练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在正方形ABCD的BC的延长线上取一点E，使CE=AC，AE交CD于F，则ÐAFC的度数为________．

     

    答案：
    解析：

    		112.5°

     


    提示：

    		利用正方形的性质

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，点E在正方形ABCD的边AB上，若EB的长为1，EC的长为2，那么正方形ABCD的面积是（　　）
    A、
    		3
    B、
    		5
    C、3
    D、5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，正方形EFGH的四个顶点在正方形ABCD的边上，若AB=a，EF=b，则△AEF的内切圆半径为
     
    ．（用含有a、b的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•达州）通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．
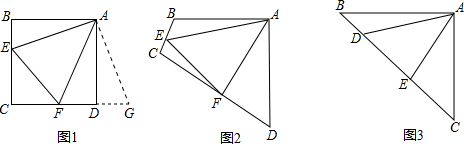
    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

    （1）思路梳理
    ∵AB=AD，
    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
    ∵∠ADC=∠B=90°，
    ∴∠FDG=180°，点F、D、G共线．
    根据
    SAS
    SAS
    ，易证△AFG≌
    △AEF
    △AEF
    ，得EF=BE+DF．
    （2）类比引申
    如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系
    ∠B+∠D=180°
    ∠B+∠D=180°
    时，仍有EF=BE+DF．
    （3）联想拓展
    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在正方形ABCD的边BC的延长线上取一点E，使CE=AC，AE交CD于点F．那么，∠ACB=
    45
    45
    °，∠E=
    22.5
    22.5
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图1，过正方形ABCD内部任意一点O作两条互相垂直的直线，分别交AD、BC于点E、F，交AB、CD于点G、H，证明：EF=GH；
    （2）当点O在正方形ABCD的边上或外部时，过点O作两条互相垂直的直线，被正方形相对的两边（或它们的延长线）截得的两条线段还相等吗？图2是其中一种情形，试就该图形对你的结论加以证明．

    查看答案和解析>>

    同步练习册答案