
如图,已知AD⊥BC于D,BG⊥BC于G,AE=AF,说明AD平分∠BAC,下面是小颖的解答过程,请补充完整。
解:∵AD⊥BC,BG⊥BC(已知)
∴∠4=∠5=90°(垂直定义)
∴__________∥____________( )
∴∠2=_______________( )
∠1=_____________( )
又∵AE=AF(已知)
∴∠3=_____________( )
∴∠1=∠2(等量代换)
∴AD平分∠BAC(角平分线定义)
 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
解:∵∠1=∠2(已知),∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )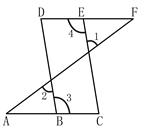
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
直线l1平行于直线l2,直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,DC∥AB交l4于点C.
(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的关系,并说明理由;
(2)当点D在l1、l2两线外侧运动时,试探究∠BAD、∠DEF、∠ADE之间的关系(点D和B、F不重合),画出图形,给出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,
试求:(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
(2)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com