
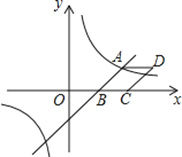
【题目】如图,已知一次函数y=![]() x-3与反比例函数
x-3与反比例函数![]() 的图象相交于点A
的图象相交于点A![]() ,与x轴相交于点B.
,与x轴相交于点B.
(1)填空: ![]() 的值为 ,
的值为 , ![]() 的值为 ;
的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)3,12;(2)(4+![]() ,3).(3)x≤-6或x>0.
,3).(3)x≤-6或x>0.
【解析】试题分析:(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数
x-3,得到n的值为3;再把点A(4,3)代入反比例函数![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比函数的性质即可得到当y≥-2时,自变量x的取值范围.
试题解析:(1)把点A(4,n)代入一次函数y=![]() x-3,可得n=
x-3,可得n=![]() ×4-3=3;
×4-3=3;
把点A(4,3)代入反比例函数![]() ,可得3=
,可得3=![]() ,
,
解得k=12.
(2)∵一次函数y=![]() x-3与x轴相交于点B,
x-3与x轴相交于点B,
∴![]() x-3=0,
x-3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,

∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3).
,3).
(3)当y=-2时,-2=![]() ,解得x=-6.
,解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,一个三角形的三个顶点的坐标,横坐标保持不变,纵坐标增加3个单位,则所得的图形与原图形相比( ).
A. 形状不变,大小扩大了3倍 B. 形状不变,向右平移了3个单位
C. 形状不变,向上平移了3个单位 D. 三角形被纵向拉伸为原来的3倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
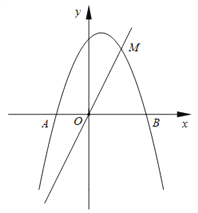
【题目】如图,在直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)已知点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,现将线段
对称,现将线段![]() 沿
沿![]() 轴向上平移
轴向上平移![]() (
(![]() >0)个单位长度.若线段
>0)个单位长度.若线段![]() 与抛物线有两个不同的公共点,试求
与抛物线有两个不同的公共点,试求![]() 的取值范围;
的取值范围;
(3)利用尺规作图,在该抛物线上作出点![]() ,使得
,使得![]() ,并简要说明理由.(保留作图痕迹)
,并简要说明理由.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DE,则∠CDF等于( ) 
A.60°
B.65°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为4cm,A为线段OP的中点,当OP=6cm时,点A与⊙O的位置关系是( )
A.A在⊙O内B.A在⊙O上C.A在⊙O外D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com