
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F. 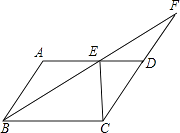
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求ABCD的面积.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,CD=AB=5,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=20°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=20°,
∴AE=AB,∠A=(180°﹣20°﹣20°)÷2=140°
(2)解:∵AE=AB=5,AD=BC=8,CD=AB=5,
∴DE=AD﹣AE=3,
∵CE⊥AD,
∴CE= ![]() =
= ![]() =4,
=4,
∴ABCD的面积=ADCE=8×4=32
【解析】(1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=20°,证出∠AEB=∠ABE=20°,由三角形内角和定理求出结果即可;(2)求出DE,由勾股定理求出CE,即可得出结果.
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.


科目:初中数学 来源: 题型:
【题目】函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是( ) 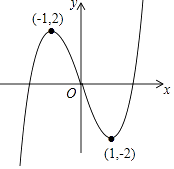
A.函数最大值为2
B.函数图象最低点为(1,﹣2)
C.函数图象关于原点对称
D.函数图象关于y轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是不在同一条直线上的三点,请按下列要求画图并作答(画图时工具不限,不需写出结论,只需画出图形、标注字母):
(1)画直线BC,连接AC;
(2)画线段BC的中点D,连接AD;
(3)画出∠ADC的平分线交AC于点E;
(4)若∠BDA=![]() 求∠ADC,∠EDC.
求∠ADC,∠EDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】报社需要在40分钟内将一篇紧急宣传文稿输入电脑.已知独立完成此项任务,小王需要50分钟,小李只需要30分钟.小王独自输入了30分钟后,因为急于完成任务,请求小李帮助他(求助时间忽略不计),他们能在要求的时间内完成任务吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
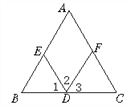
【题目】如图,(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: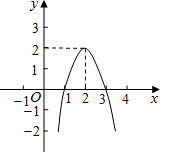
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c+k=0有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试根据图中信息,解答下列问题.
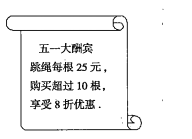
(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com