
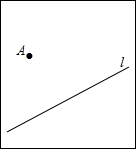
 点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:
点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由: 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
 已知a、b、c在数轴上的位置如图所示:
已知a、b、c在数轴上的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a,b,c在数轴上的位置如图所示,若代数式|-c|+6|b-a|+|2a-b-c|-|5b+2c-1|化简后的值为17,那么当x=-1时,求代数式12ax-3bx3-5的值.
已知a,b,c在数轴上的位置如图所示,若代数式|-c|+6|b-a|+|2a-b-c|-|5b+2c-1|化简后的值为17,那么当x=-1时,求代数式12ax-3bx3-5的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
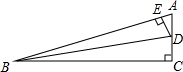 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10000 m | B. | 1000 m | C. | 100 m | D. | 10 m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3与点A、B、C,直线DF分别交l1、l2、l3与点D、E、F,AC与DF相交于点H,如果AH=2,BH=1,BC=5,那么$\frac{DE}{EF}$的值等于( )
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3与点A、B、C,直线DF分别交l1、l2、l3与点D、E、F,AC与DF相交于点H,如果AH=2,BH=1,BC=5,那么$\frac{DE}{EF}$的值等于( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
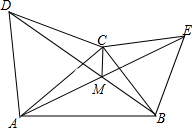 如图,已知在△ABC中,分别以AC、BC为边向外作正△BCE,正△ACD,BD与AE交于M.
如图,已知在△ABC中,分别以AC、BC为边向外作正△BCE,正△ACD,BD与AE交于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com