
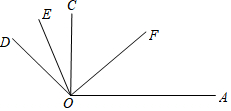
 如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,∠EOF=60°.
如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,∠EOF=60°.  夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
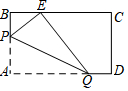 如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.
如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
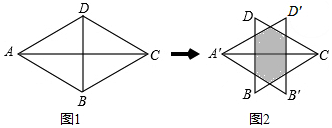
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
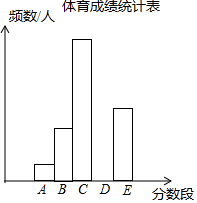 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
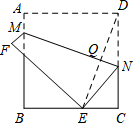 如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.
如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com