
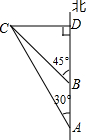
 如图所示,一艘轮船以30海里/小时的速度向正北方向航行,在A处得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处时测得灯塔C在北偏西45°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.
如图所示,一艘轮船以30海里/小时的速度向正北方向航行,在A处得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处时测得灯塔C在北偏西45°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离. ≈1.41,
≈1.41, ≈1.73)
≈1.73) 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
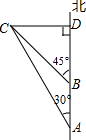 如图所示,一艘轮船以30海里/小时的速度向正北方向航行,在A处得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处时测得灯塔C在北偏西45°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.
如图所示,一艘轮船以30海里/小时的速度向正北方向航行,在A处得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处时测得灯塔C在北偏西45°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
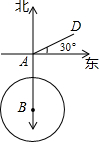 (1998•河北)如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,台风中心20
(1998•河北)如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,台风中心20| 10 |
| 13 |
查看答案和解析>>
科目:初中数学 来源:黑龙江省中考真题 题型:解答题
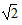 ≈1.41,
≈1.41,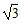 ≈1.73)
≈1.73) 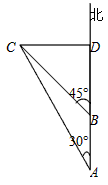
查看答案和解析>>
科目:初中数学 来源:1998年河北省中考数学试卷(解析版) 题型:解答题
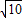 海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.
海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里. ≈3.6)?
≈3.6)?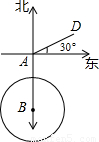
查看答案和解析>>
科目:初中数学 来源:2011年黑龙江省大庆市中考数学试卷(解析版) 题型:解答题
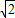 ≈1.41,
≈1.41,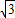 ≈1.73)
≈1.73)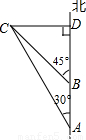
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com