
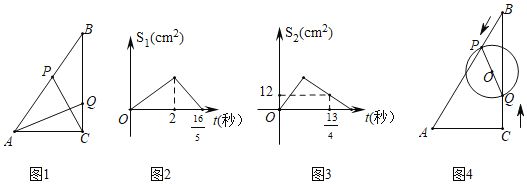
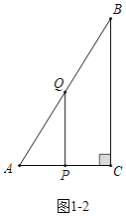
ΓΨΧβΡΩΓΩ»γΆΦΘ®1Θ©Θ§‘ΎRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫ6cmΘ§Ε·ΒψP¥”ΒψB≥ωΖΔΘ§―Ί’έœΏBΓζAΓζC¬ΖœΏ‘»ΥΌ‘ΥΕ·ΒΫCΆΘ÷ΙΘ§Ε·ΒψQ¥”ΒψC≥ωΖΔΘ§―Ί’έœΏCΓζBΓζA¬ΖœΏ‘»ΥΌ‘ΥΕ·ΒΫAΆΘ÷ΙΘ§»γΒψPΓΔQΆ§ ±≥ωΖΔ‘ΥΕ·tΟκΚσΘ§»γΆΦΘ®2Θ© «ΓςBPCΒΡΟφΜΐS1Θ®cm2Θ©”κtΘ®ΟκΘ©ΒΡΚ· ΐΙΊœΒΆΦœσΘ§ΆΦΘ®3Θ© «ΓςAQCΒΡΟφΜΐS2Θ®cm2Θ©”κtΘ®ΟκΘ©ΒΡΚ· ΐΙΊœΒΆΦœσΘΚ
Θ®1Θ©ΒψP‘ΥΕ·ΥΌΕ»ΈΣΓΓ ΓΓcm/ΟκΘΜQ‘ΥΕ·ΒΡΥΌΕ»ΓΓ ΓΓcm/ΟκΘΜ
Θ®2Θ©Ν§Ϋ”PQΘ§Β±tΈΣΚΈ÷Β ±Θ§PQΓΈBCΘΜ
Θ®3Θ©»γΆΦΘ®4Θ©Β±‘ΥΕ·tΘ®0ΓήtΓή2Θ©Οκ ±Θ§ «Ζώ¥φ‘Ύ’β―υΒΡ ±ΩΧΘ§ Ι“‘PQΈΣ÷±ΨΕΒΡΓ―O”κRtΓςABCΒΡ“ΜΧθ±Ώœύ«–Θ§»τ¥φ‘ΎΘ§«σ≥ωtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©5Θ§4ΘΜΘ®2Θ©tΘΫ![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§tΒΡ÷ΒΈΣ
ΘΜΘ®3Θ©¥φ‘ΎΘ§tΒΡ÷ΒΈΣ![]() Μρ1Μρ
Μρ1Μρ![]() Μρ0Θ°
Μρ0Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί¬Ζ≥ΧΘ§ΥΌΕ»Θ§ ±Φδ÷°ΦδΒΡΙΊœΒΫαΚœ“―÷ΣΧθΦΰΫβΨωΈ ΧβΦ¥Ω…ΘΜ
Θ®2Θ©»γΆΦ1©¹2÷–Θ§Β±PQΓΈAC ±Θ§‘ρ”–![]() Θ§”…¥ΥΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ§”…¥ΥΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
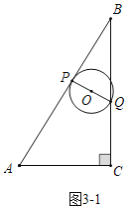
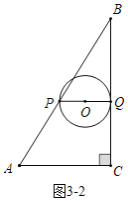
Θ®3Θ©Ζ÷»ΐ÷÷«ι–ΈΔΌ»γΆΦ3©¹1÷–Θ§Β±Γ―O”κABœύ«– ±Θ§QPΓΆABΘ°ΔΎ»γΆΦ3©¹2÷–Θ§Β±Γ―O”κBCœύ«– ±Θ§QPΓΆBCΘ°Δέ»γΆΦ3©¹3÷–Θ§Β±Γ―O”κACœύ«– ±Θ§…η«–ΒψΈΣHΘ§Ν§Ϋ”OHΘ°ΉςPMΓΆAC”ΎMΘ§PKΓΆBC”ΎKΘ°Ζ÷±πΙΙΫ®ΖΫ≥Χ«σΫβΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©”…ΆΦ2Ω…÷ΣΘ§Βψ![]() ¥”
¥”![]() ‘ΥΕ·ΒΫ
‘ΥΕ·ΒΫ![]() ΒΡ ±Φδ
ΒΡ ±Φδ![]() ΟκΘ§
ΟκΘ§
![]() Βψ
Βψ![]() ΒΡ‘ΥΕ·ΥΌΕ»
ΒΡ‘ΥΕ·ΥΌΕ»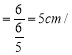 ΟκΘ°
ΟκΘ°
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
»γΆΦ![]() ÷–Θ§Ής
÷–Θ§Ής![]() ”Ύ
”Ύ![]() Θ°
Θ°
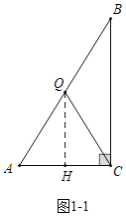
”…ΆΦ3Ω…÷ΣΘ§![]() ±Θ§
±Θ§![]() ΒΡΟφΜΐΈΣ12Θ§
ΒΡΟφΜΐΈΣ12Θ§
![]()
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Βψ
Βψ![]() ΒΡ‘ΥΕ·ΥΌΕ»
ΒΡ‘ΥΕ·ΥΌΕ»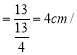 ΟκΘ°
ΟκΘ°
Ι ¥πΑΗΈΣ5Θ§4ΘΜ
Θ®2Θ©»γΆΦ![]() ÷–Θ§Β±
÷–Θ§Β±![]() ±Θ§‘ρ”–
±Θ§‘ρ”–![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
![]() Β±
Β±![]() Οκ ±Θ§
Οκ ±Θ§![]() Θ°
Θ°
Θ®3Θ©ΔΌ»γΆΦ![]() ÷–Θ§Β±
÷–Θ§Β±![]() ”κ
”κ![]() œύ«– ±Θ§
œύ«– ±Θ§![]() Θ°
Θ°
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]()
ΔΎ»γΆΦ![]() ÷–Θ§Β±
÷–Θ§Β±![]() ”κ
”κ![]() œύ«– ±Θ§
œύ«– ±Θ§![]() Θ°
Θ°
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ°
Θ°
Δέ»γΆΦ![]() ÷–Θ§Β±
÷–Θ§Β±![]() ”κ
”κ![]() œύ«– ±Θ§…η«–ΒψΈΣ
œύ«– ±Θ§…η«–ΒψΈΣ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§
Ής![]() ”Ύ
”Ύ![]() Θ§
Θ§![]() ”Ύ
”Ύ![]() Θ°
Θ°
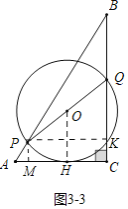
‘ρ![]() Θ§
Θ§![]() Θ§
Θ§
”…Χβ“β![]() Θ§
Θ§![]() Θ§
Θ§
![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§
«ΨΊ–ΈΘ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§‘ρ”–
÷–Θ§‘ρ”–![]() Θ§
Θ§
ΫβΒΟ![]() Μρ0Θ§
Μρ0Θ§
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡ![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() Μρ1Μρ
Μρ1Μρ![]() Μρ0Θ°
Μρ0Θ°


 ΚΘΒμΜΤΗ‘Οϊ ΠΒΦΚΫœΒΝ–¥πΑΗ
ΚΘΒμΜΤΗ‘Οϊ ΠΒΦΚΫœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
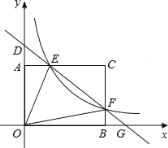
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈAOBCΒΡΕΞΒψΉχ±ξΖ÷±πΈΣAΘ®0Θ§3Θ©Θ§OΘ®0Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§CΘ®4Θ§3Θ©Θ§Ε·ΒψF‘Ύ±ΏBC…œΘ®≤Μ”κB.C÷ΊΚœΘ©Θ§ΙΐΒψFΒΡΖ¥±»άΐΚ· ΐyΘΫ![]() ΒΡΆΦœσ”κ±ΏACΫΜ”ΎΒψEΘ§÷±œΏEFΖ÷±π”κy÷αΚΆx÷αœύΫΜ”ΎΒψDΚΆGΘ°Ηχ≥ωœ¬Ν–ΟϋΧβΘΚΔΌ»τk=4Θ§‘ρΓςOEFΒΡΟφΜΐΈΣ
ΒΡΆΦœσ”κ±ΏACΫΜ”ΎΒψEΘ§÷±œΏEFΖ÷±π”κy÷αΚΆx÷αœύΫΜ”ΎΒψDΚΆGΘ°Ηχ≥ωœ¬Ν–ΟϋΧβΘΚΔΌ»τk=4Θ§‘ρΓςOEFΒΡΟφΜΐΈΣ![]() ΘΜΔΎ»τkΘΫ
ΘΜΔΎ»τkΘΫ![]() Θ§‘ρΒψCΙΊ”Ύ÷±œΏEFΒΡΕ‘≥ΤΒψ‘Ύx÷α…œΘΜΔέ¬ζΉψΧβ…ηΒΡkΒΡ»Γ÷ΒΖΕΈß «0ΘΦkΓή12ΘΜΔή»τDEEG=
Θ§‘ρΒψCΙΊ”Ύ÷±œΏEFΒΡΕ‘≥ΤΒψ‘Ύx÷α…œΘΜΔέ¬ζΉψΧβ…ηΒΡkΒΡ»Γ÷ΒΖΕΈß «0ΘΦkΓή12ΘΜΔή»τDEEG=![]() Θ§‘ρk=1Θ°Τδ÷–’ΐ»ΖΒΡΟϋΧβΒΡ–ρΚ≈ «____________Θ®Χν–ρΚ≈Θ©Θ°
Θ§‘ρk=1Θ°Τδ÷–’ΐ»ΖΒΡΟϋΧβΒΡ–ρΚ≈ «____________Θ®Χν–ρΚ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
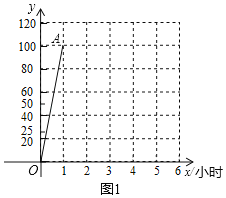
ΓΨΧβΡΩΓΩ―–ΨΩ±μΟςΘΚ»ΥΕ‘ ¬ΈοΒΡ»œ ΕΖ÷≥…Φ«“δΚΆ“≈ΆϋΝΫΗωΫΉΕΈΘ§Φ¥«ΩΜ·Φ«“δ÷ΝΦ«“δΝΩΈΣ100ΘΜ»ΜΚσΆΘ÷Ι«ΩΜ·Φ«“δΘ§ΩΣ Φ“≈ΆϋΘ°»γΆΦ1÷–ΒΡœΏΕΈOA «–ΓΟς‘Ύ1–Γ ±÷°ΡΎΕ‘Ρ≥ΤΣΈΡ’¬Ϋχ––«ΩΜ·Φ«“δ ±–ΓΟςΒΡΦ«“δΝΩy”κ ±Φδx–Γ ±÷°ΦδΒΡΚ·–ßΆΦœσΘΜΒ±–ΓΟςΆΘ÷Ι«ΩΜ·Φ«“δΚσΘ§Φ«“δΝΩy”κ ±Φδx–Γ ±ΒΡ±δΜ·«ιΩω»γœ¬±μΘ®ΆΦ2Θ©Υυ ΨΘΚ
Θ®1Θ©Α―ΆΦ2Υυ ΨΒΡ±μ÷–Θ®xΘ§yΘ©ΒΡΗςΉιΕ‘”Π÷ΒΉςΈΣΒψΒΡΉχ±ξΘ§‘Ύ»γΆΦ1Υυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Οη≥ωΗςΒψΘ§≤Δ”Ο“ΜΧθΤΫΜ§ΒΡ«ζœΏΥ≥¥ΈΝ§Ϋ”Θ§Ιέ≤λΥυΜ≠ΒΡΆΦœσΘ§≤¬≤β–ΓΟςΆΘ÷Ι«ΩΜ·Φ«“δΚσ «ΙΊ”ΎxΒΡ ≤Ο¥Κ· ΐΘ§≤Δ«σ≥ωΗΟΚ· ΐΫβΈω ΫΘ°
Θ®2Θ©―–ΨΩ±μΟςΘΚΒ±Φ«“δΝΩ‘Ύ75“‘…œΘ®Κ§75Θ© ±Θ§≥ΤΈΣ λΦ«Θ°«κΈ ΘΚ–ΓΟςΙ≤”–Εύ…ΌΖ÷÷”Ε‘“ΜΤΣΈΡ’¬Έ§≥÷ λΦ«≥ΧΕ»ΘΩ
¥”ΩΣ ΦΦ«“δΥυΨ≠άζΒΡ ±Φδx/–Γ ± | 1 | 2 | 3 | 4 |
―ß…ζΒΡΦ«“δΝΩy | 100 | 50 | 25 | 20 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
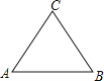
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒ»±ΏΓςABC÷–±ΏAB=10Θ§Α¥“Σ«σΫβ¥πΘΚ
Θ®1Θ©≥ΏΙφΉςΆΦΘΚΉςΓœPBAΘ§ ΙΒΟΓœPBA=30ΓψΘ§…δœΏBPΫΜ±ΏAC”ΎΒψPΘ§Θ®≤Μ–¥ΉςΖ®Θ§±ΘΝτΉςΆΦΚέΦΘΘ©Θ°
Θ®2Θ©‘Ύ…œΆΦ÷–Θ§»τΒψD‘Ύ…δœΏBP…œΘ§«“ ΙΒΟAD=5![]() Θ§«σBDΒΡ≥ΛΘ®ΫαΙϊ±ΘΝτΗυΚ≈Θ©Θ°
Θ§«σBDΒΡ≥ΛΘ®ΫαΙϊ±ΘΝτΗυΚ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ®m©¹1Θ©x2+Θ®m©¹2Θ©x©¹1ΘΫ0Θ®mΈΣ Β ΐΘ©Θ°
Θ®1Θ©»τΖΫ≥Χ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§«σmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τm «’ϊ ΐΘ§«“ΖΫ≥Χ”–ΝΫΗω≤ΜœύΒ»ΒΡ’ϊ ΐΗυΘ§«σmΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§![]() Ζ÷±π«–
Ζ÷±π«–![]() ”ΎΒψ
”ΎΒψ![]() ΒψΘ°
ΒψΘ°
Θ®1Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ή≥ΛΘ°
ΒΡ÷ή≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷ήάœ ΠΈΣΝΥΝΥΫβ―ß…ζΉ‘÷ς―ßœΑΓΔΚœΉςΫΜΝςΒΡΨΏΧε«ιΩωΘ§Ε‘±ΨΑύ≤ΩΖ÷―ß…ζΫχ––ΝΥΈΣΤΎΑκΡξΒΡΗζΉΌΒς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΖ÷≥…ΥΡάύAΘΚ”≈ΘΜBΘΚΝΦΘΜCΘΚ÷–ΘΜDΘΚ≤νΘ°“άΨίΒς≤ιΫαΙϊΜφ÷Τ≥…“‘œ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΡψΗυΨίΆ≥ΦΤΆΦΫβ¥πœ¬Ν–Έ ΧβΘΚ
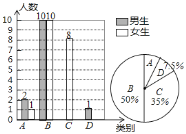
Θ®1Θ©±Ψ¥ΈΒς≤ι÷–Θ§÷ήάœ Π“ΜΙ≤Βς≤ιΝΥ______Οϊ―ß…ζΘΜ
Θ®2Θ©ΫΪΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©ΈΣΝΥΙ≤Ά§Ϋχ≤ΫΘ§÷ήάœ Πœκ¥”±ΜΒς≤ιΒΡAάύΚΆDάύ―ß…ζ÷–Ζ÷±π―ûÓ̸̢§―ßΫχ––ΓΑ“ΜΕ‘“ΜΓ±ΑοΖωΘ§«κ”ΟΝ–±μΖ®ΜρΜ≠ ς–ΈΆΦΒΡΖΫΖ®«σΥυ―ΓΒΡΝΫΈΜΆ§―ß«ΓΚΟ «ΝΫΈΜ≈°Ά§―ßΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
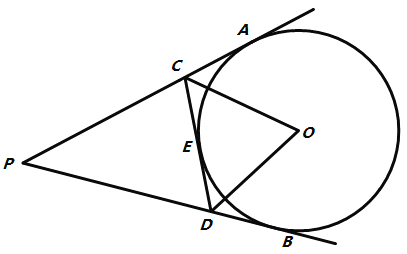
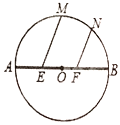
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() ΒΡ÷±ΨΕ
ΒΡ÷±ΨΕ![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() ΈΣ
ΈΣ![]() ΒΡ»ΐΒ»Ζ÷ΒψΘ§
ΒΡ»ΐΒ»Ζ÷ΒψΘ§![]() ΓΔ
ΓΔ![]() ΈΣ
ΈΣ![]() …œΝΫΒψΘ§«“
…œΝΫΒψΘ§«“![]()
![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐyΘΫax2ΘΪbxΘΪcΘ®aΘΦ0Θ©ΒΡΆΦœσΨ≠ΙΐΘ®mΘΪ1Θ§aΘ©Θ§Θ®mΘ§bΘ©ΝΫΒψ.
Θ®1Θ©»τmΘΫ1Θ§aΘΫΘ≠1Θ§«σΗΟΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σ÷ΛΘΚamΘΪbΘΫ0ΘΜ
Θ®3Θ©»τΗΟΕΰ¥ΈΚ· ΐΒΡΉν¥σ÷ΒΈΣ![]() Θ§Β±xΘΫ1 ±Θ§yΓί3aΘ§«σaΒΡ»Γ÷ΒΖΕΈß.
Θ§Β±xΘΫ1 ±Θ§yΓί3aΘ§«σaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com