Question

亲爱的同学，你准备好了吗？让我们一起进行一次研究性学习：研究用一条直线等分几何图形的面积．我们很容易发现这样一个事实：
如图①，对于三角形ABC，取BC边的中点D，过A，D两点画一条直线，即可把△ABC分为面积相等的两部分．

（1）如图②，对于平行四边形ABCD，如何画一条直线把平行四边形ABCD分为面积相等的两部分．
答：______（写出一种方案即可）．理由是：______．
（2）受上面的启发，请你研究以下两个问题：
①如图③，一块平行四边形的稻田里有一个圆形的蓄水池，现要从蓄水池引一条笔直的水渠，并使蓄水池两侧的稻田面积相等，请你画出你的设计方案，保留作图痕迹，不必说明理由．
②某农业研究所有一块梯形形状的实验田如图3④，准备把这块实验田种上面积相同的西红柿和青椒（都是新品种），应该如何分割，请你分别在图3④、图3⑤中设计两种不同的分割方案，并说明理由．

Answer 1

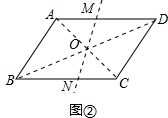
解：（1）连接两对角线AC、BD交于点O，过O点任作一直线MN即可（如图）．
（不妨设该直线与AD、BC分别交于点M、N）
理由：∵四边形ABCD是平行四边形，∴AO=CO，AD∥BC，
∴∠MAO=∠NCO，
又∵∠AOM=∠CON，
∴△AOM≌△CON．
∴S_△AMO=S_△CNO．
同理得S_△MOD=S_△NOB．
又易得S_△AOB=S_△COD，
所以S_{四边形MNCD}=S_{四边形ABNM}．

（2）①如图，
②
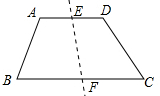
方案一：分别取AD、BC的中点E、F，连接EF，线段EF就是所求作的分割线．
理由：∵AE=ED，BF=FC，
∴S_{四边形ABEF}=（AE+BF）•h，
=（ED+FC）•h，
=S_{四边形EFCD}，

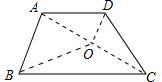
方案二：连接AC，取中点O，连接BO、OD，折线BOD可以把梯形分割为两个面积相等的图形．
理由：∵AO=OC，∴S_△AOB=S_△BOC，S_△DOC=S_△ADO，
∴S_△AOB+S_△AOD=S_△BOC+S_△DOC．

分析：（1）利用平行四边形的性质得出即可得出连接两对角线AC、BD交于点O，过O点任作一直线MN即可，再利用△AOM≌△CON得出即可；
（2）①找到水池圆心以及平行四边形对角线交点即可得出答案；
②分别取AD、BC的中点E、F，连接EF，线段EF就是所求作的分割线或连接AC，取中点O，连接BO、OD，折线BOD可以把梯形分割为两个面积相等的图形．
点评：此题主要考查了应用与设计作图中分割图形面积，利用三角形中线能平分三角形面积得出是解题关键．