
 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
分析 根据矩形性质得出AC=2AO,BD=2BO,AC=BD,推出AO=OB,得出等边三角形AOB,得出AC,由勾股定理求出BC,即可求出矩形ABCD的面积.
解答 解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,∠ABC=90°,
∴AO=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AC=2AO=8,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4$\sqrt{3}$,
∴矩形ABCD的面积=AB•BC=4×4$\sqrt{3}$=16$\sqrt{3}$.
故选:A.
点评 本题考查了等边三角形的性质和判定,矩形的性质的应用,勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | 3 | 5 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 2 | 4 | 2 | 5 | 1 |
| A. | 47,49 | B. | 48,49 | C. | 47.5,49 | D. | 48,50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
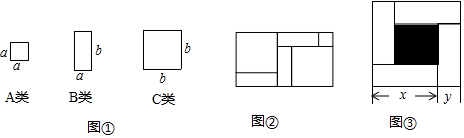
 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张全等的等腰直角三角形纸片,面积都为2,另两张是全等的直角三角形纸片,中间一张是正方形纸片,则这个平行四边形的面积是8.
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张全等的等腰直角三角形纸片,面积都为2,另两张是全等的直角三角形纸片,中间一张是正方形纸片,则这个平行四边形的面积是8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
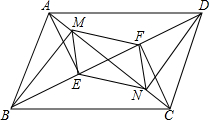 如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.
如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com