
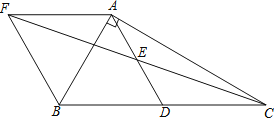
【题目】如图,在△ABC中,∠BAC=90°,AB=4,tan∠ACB=![]() ,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.
,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.
【答案】12
【解析】根据AF∥BC,证明△AEF≌△DEC(AAS),得到AF=CD,可证四边形AFBD是平行四边形,所以S四边形AFBD=2S△ABD,又因为BD=DC,所以S△ABC=2S△ABD,所以S四边形AFBD=S△ABC,从而求出答案.
∵AF∥BC,
∴∠AFC=∠FCD,
在△AEF与△DEC中, ,
,
∴△AEF≌△DEC(AAS).
∴AF=DC,
∵BD=DC,
∴AF=BD,
∴四边形AFBD是平行四边形,
∴S四边形AFBD=2S△ABD,
又∵BD=DC,
∴S△ABC=2S△ABD,
∴S四边形AFBD=S△ABC,
∵∠BAC=90°,tan∠ACB=![]() ,AB=4,
,AB=4,
∴AC=![]() =6,
=6,
∴S△ABC=![]() ABAC=
ABAC=![]() ×4×6=12,
×4×6=12,
∴S四边形AFBD=12.
故答案为:12.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在沙滩上用石子摆成的小房子

观察图形的变化规律,则第10个小房子用了( )颗石子.
A. 119 B. 121 C. 140 D. 142
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系.
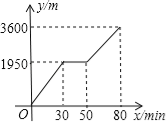
(1)小亮行走的总路程是 m,他途中休息了 min;
(2)①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l依次三点A、B、C,AB=6,BC=m,点M是AC点中点,
(1)如图,当m=4,求线段BM的长度(写清线段关系);
(2)在直线l上一点D,CD=n < m,用m、n表示线段DM的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是马小哈同学做的一道题:
解方程:![]()
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得![]()
(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com