
【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E.
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(0<x< ![]() ),四边形BPEC的面积为y,求证:y=
),四边形BPEC的面积为y,求证:y= ![]() (
( ![]() ﹣x)2 .
﹣x)2 .
【答案】
(1)证明:作PG⊥BC于G,PH⊥CD于H, 
∵四边形ABCD是正方形,正方形是轴对称图形,
∴PB=PD,PG=PH,∠BCD=90°,
∴四边形PGCH是矩形,
∴PG⊥PH,又PE⊥PB,
∴∠BPG=∠EPH,
在△BPG和△EPH中,
 ,
,
∴△BPG≌△EPH,
∴PB=PE,又PB=PD,
∴PE=PD
(2)解:∵四边形ABCD是轴对称图形,
∴∠BPC=∠DPC,∠GPC=∠HPC=45°,
∴∠BPG=∠DPH,又∠BPG=∠EPH,
∴∠DPH=∠EPH,又PH⊥CD,
∴DH=EH= ![]() DE=
DE= ![]() CD=
CD= ![]() ,
,
∴PH=HC= ![]() ,
,
∴PC= ![]() ,
,
∵正方形ABCD的边长为1,
∴AC= ![]() ,
,
∴AP=AC﹣PC= ![]()
(3)证明:∵AC= ![]() ,AP=x,
,AP=x,
∴PC= ![]() ﹣x,
﹣x,
∵△BPG≌△EPH,
∴四边形BPEC的面积y=正方形PGCH的面积= ![]() (
( ![]() ﹣x)2.
﹣x)2.
【解析】(1)证线段相等可证全等,因此需作垂线构造全等三角形;(2)求AP可转化为求PC, 可利用正方形的性质和勾股定理即可;(3)通过证出全等转化不规则四边形为规则的正方形.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简)
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的![]() 满足
满足![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
A.小明调查了100名同学
B.所得数据的众数是40小时
C.所得数据的中位数是30小时
D.全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
(1)如图1,∠AEM,∠M,∠CFM的数量关系为________;(直接写出答案)
(2)如图2,∠MEB和∠MFD的角平分线交于点N,若∠EMF等于130°,求∠ENF的度数;
(3)如图3,点G为直线CD上一点,延长GM交直线AB于点Q,点P为MG上一点,射线PF、EH相交于点H,满足![]() ,
,![]() ,设∠EMF=α,求∠H的度数(用含α的代数式表示).
,设∠EMF=α,求∠H的度数(用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )
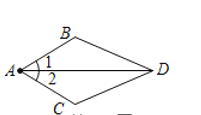
A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.
(1)写出点E的纵坐标.
(2)求证:BD=OE;
(3)如图2,连接DE交AB于F.求证:F为DE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.
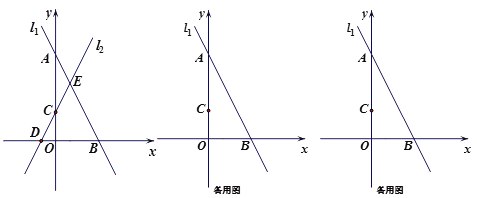
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1,并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2,且A2(a,2),C2(-2,b),求a+b的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com