
【题目】如图,在平行四边形ABCD的边AD的延长线上截取DE=AD,F是AE延长线上的一点,连结BD、CE、BF分别交CE、CD于G、H.
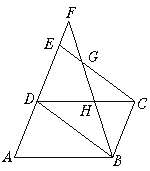
求证:(1)△ABD≌△DCE;
(2)CE∶CG=DF∶AD.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行四边形的性质得到DC=AB,∠EDC=∠DAB,再根据DE=AD,即可证明△ABD≌△DCE;
(2)先证明四边形DBCE是平行四边形,根据平行的性质得到∠CGB=∠DBF
证明:(1) ∵四边形DBCE为平行四边形,
∴DC=AB,∠EDC=∠DAB,
又∵DE=AD,
在△ABD和△DCE中,
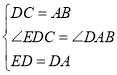
所以△ABD≌△DCE(SAS);
(2)∵四边形ABCD是平行四边形,F是AE延长线上的一点,
∵DE=AD,DE∥BC,
∴DE=AD=BC(等量替换),
∴四边形DBCE是平行四边形,
∴EC∥DB,∠GCB=∠BDF,
∴∠CGB=∠DBF,
∴△DBF∽△CGB,
由△DBF∽△CGB,可得![]() ,
,
又∵CE=DB,CB=AD,
∴![]() ,
,
即CE∶CG=DF∶AD.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】体育锻炼对学生的健康成长有着深远的影响.某中学 开展了四项球类活动:A:乒乓球;B:足球;C:排球;D:篮球.王老师对学生最喜欢的一项球类活动进行了抽样调查(每人只限一项),并将调查结果绘制成图 1,图2两幅不完整的统计图.
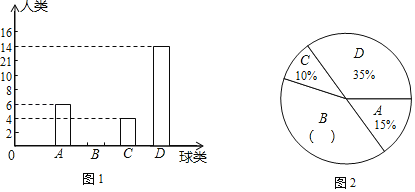
请根据图中信息解答下列问题:
(1)参加此次调查的学生总数是 人;将图1、图2的统计图补充完整;
(2)已知在被调查的最喜欢排球项目的4名学生中只有1名女生,现从这4名学生中任意抽取2名学生参加校排球队,请用列表法或画树状图的方法,求出恰好抽到一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
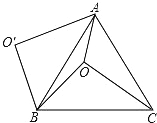
①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;
②连接OO′,则OO′=4;
③∠AOB=150°;
④S四边形AOBO′=6+4![]() .
.
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
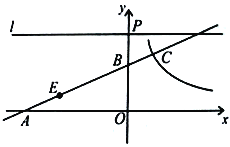
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在江苏省某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上.

(1)MN是否穿过原始森林保护区?为什么?(参考数据:![]() )
)
(2)若修路工程工程需尽快完成.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.求甲、乙两工程队单独完成此项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+4x+2.
(1)若函数图象与x轴只有一个交点,求m的值;
(2)是否存在整数m,使函数图象与x轴有两个交点,且两交点横坐标差的平方等于8?若存在,求出符合条件的m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某中学积极响应创建全国文明城市活动,举办了以“校园文明”为主题的手抄报比赛.所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如右两幅统计图.请你根据图中所给信息解答意)
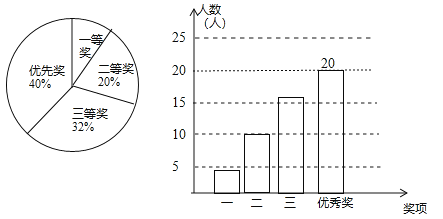
(1)等奖所占的百分比是________;三等奖的人数是________人;
(2)据统计,在获得一等奖的学生中,男生与女生的人数比为![]() ,学校计划选派1名男生和1名女生参加市手抄报比赛,请求出所选2位同学恰是1名男生和1名女生的概率;
,学校计划选派1名男生和1名女生参加市手抄报比赛,请求出所选2位同学恰是1名男生和1名女生的概率;
(3)学校计划从获得二等奖的同学中选取一部分人进行集训使其提升为一等奖,要使获得一等奖的人数不少于二等奖人数的2倍,那么至少选取多少人进行集训?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两组卡片共5张,
两组卡片共5张,![]() 组中三张分别写有数字2、4、6,
组中三张分别写有数字2、4、6,![]() 组中两张分别写有数字3、5,它们除数字外其他都相同.
组中两张分别写有数字3、5,它们除数字外其他都相同.
(1)随机从![]() 组中抽取一张,则抽到数字是2的概率为______;
组中抽取一张,则抽到数字是2的概率为______;
(2)分别随机从![]() 组、
组、![]() 组中各抽取一张.现制定这样一个游戏规则:若所抽取的两个数字之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?请你用画树状图或列表的方法计算并说明理由.
组中各抽取一张.现制定这样一个游戏规则:若所抽取的两个数字之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?请你用画树状图或列表的方法计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为□ABCD中一点,EA=ED,∠AED=90,点F,G分别为AB,BC上的点,连接DF,AG,AD=AG=DF,且AG⊥DF于点H,连接EG,DG,延长AB,DG相交于点P.
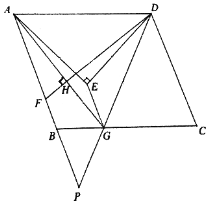
(1)若AH=6,FH=2,求AE的长;
(2)求证:∠P=45;
(3)若DG=2PG,求证:∠AGE=∠EDG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com