
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏyΘΫax2+bx+5”κx÷αΫΜ”ΎAΘ®©¹1Θ§0Θ©Θ§BΘ®5Θ§0Θ©ΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ°
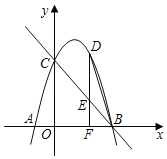
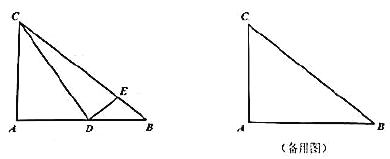
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΒψD «ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ®”κΒψCΘ§B≤Μ÷ΊΚœΘ©Θ§ΙΐΒψDΉςDFΓΆx÷α”ΎΒψFΘ§ΫΜ÷±œΏBC”ΎΒψEΘ§Ν§Ϋ”BDΘ§÷±œΏBCΡήΖώΑ―ΓςBDFΖ÷≥…ΟφΜΐ÷°±»ΈΣ2ΘΚ3ΒΡΝΫ≤ΩΖ÷ΘΩ»τΡήΘ§«κ«σ≥ωΒψDΒΡΉχ±ξΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©»τMΈΣ≈ΉΈοœΏΕ‘≥Τ÷α…œ“ΜΕ·ΒψΘ§ ΙΒΟΓςMBCΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ©¹x2+4x+5ΘΜΘ®2Θ©Β±ΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ© ±Θ§÷±œΏBCΑ―ΓςBDFΖ÷≥…ΟφΜΐ÷°±»ΈΣ2ΘΚ3ΒΡΝΫ≤ΩΖ÷ΘΜΘ®3Θ©¬ζΉψΧθΦΰΒΡMΒψΒΡΉχ±ξΈΣΘ®2Θ§7Θ©Θ§Θ®2Θ§©¹3Θ©Θ§Θ®2Θ§6Θ©Θ§Θ®2Θ§©¹1Θ©Θ°
Θ© ±Θ§÷±œΏBCΑ―ΓςBDFΖ÷≥…ΟφΜΐ÷°±»ΈΣ2ΘΚ3ΒΡΝΫ≤ΩΖ÷ΘΜΘ®3Θ©¬ζΉψΧθΦΰΒΡMΒψΒΡΉχ±ξΈΣΘ®2Θ§7Θ©Θ§Θ®2Θ§©¹3Θ©Θ§Θ®2Θ§6Θ©Θ§Θ®2Θ§©¹1Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…≈ΉΈοœΏ”κx÷αΒΡΝΫΗωΫΜΒψΉχ±ξ¥ζ»κΫβΈω Ϋ÷–Ν–≥ωΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉι![]() Θ§Ϋβ¥ΥΖΫ≥ΧΉιΦ¥Ω…«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ§Ϋβ¥ΥΖΫ≥ΧΉιΦ¥Ω…«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫαΚœΆΦœώΩ…÷ΣΓςBDEΚΆΓςBEF «Β»ΗΏΒΡΘ§Θ§”…¥ΥΒΟ≥ωΥϊΟ«ΒΡΟφΜΐ±»Φ¥ΈΣDEΘΚEFΘΫ2ΘΚ3Θ§Ζ÷ΝΫ÷÷«ιΩωΩΦ¬«Θ§ΗυΨίΝΫΒψΦδΒΡΨύάκΙΪ ΫΦ¥Ω…ΒΟ≥ωΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σΒΟDΒψΉχ±ξΘΜ
Θ®3Θ©Ζ÷«ιΩωΖ÷ΈωΓςMBCΈΣ÷±Ϋ«»ΐΫ«–Έ ±MΒΡΉχ±ξΦ¥Ω….
Θ®1Θ©ΫΪAΘ®©¹1Θ§0Θ©Θ§BΘ®5Θ§0Θ©¥ζ»κyΘΫax2+bx+5Θ§
ΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
‘ρ≈ΉΈοœΏΫβΈω ΫΈΣyΘΫ©¹x2+4x+5ΘΜ
Θ®2Θ©ΡήΘ°
…η÷±œΏBCΒΡΫβΈω ΫΈΣyΘΫkx+bΘ§
Α―CΘ®0Θ§5Θ©Θ§BΘ®5Θ§0Θ©¥ζ»κΒΟ![]()
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
Υυ“‘÷±œΏBCΒΡΫβΈω ΫΈΣyΘΫ©¹x+5Θ§
…ηDΘ®xΘ§©¹x2+4x+5Θ©Θ§‘ρEΘ®xΘ§©¹x+5Θ©Θ§FΘ®xΘ§0Θ©Θ§Θ®0ΘΦxΘΦ5Θ©Θ§
ΓύDEΘΫ©¹x2+4x+5©¹Θ®©¹x+5Θ©ΘΫ©¹x2+5xΘ§EFΘΫ©¹x+5Θ§
Β±DEΘΚEFΘΫ2ΘΚ3 ±Θ§SΓςBDEΘΚSΓςBEFΘΫ2ΘΚ3Θ§
Φ¥Θ®©¹x2+5xΘ©ΘΚΘ®©¹x+5Θ©ΘΫ2ΘΚ3Θ§
’ϊάμΒΟ3x2©¹17x+10ΘΫ0Θ§
ΫβΒΟx1ΘΫ![]() Θ§x2ΘΫ5Θ®…α»ΞΘ©Θ§¥Υ ±DΒψΉχ±ξΈΣΘ®
Θ§x2ΘΫ5Θ®…α»ΞΘ©Θ§¥Υ ±DΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Β±DEΘΚEFΘΫ3ΘΚ2 ±Θ§SΓςBDEΘΚSΓςBEFΘΫ3ΘΚ2Θ§Φ¥Θ®©¹x2+5xΘ©ΘΚΘ®©¹x+5Θ©ΘΫ3ΘΚ2Θ§
’ϊάμΒΟ2x2©¹13x+15ΘΫ0Θ§
ΫβΒΟx/span>1ΘΫ![]() Θ§x2ΘΫ5Θ®…α»ΞΘ©Θ§¥Υ ±DΒψΉχ±ξΈΣΘ®
Θ§x2ΘΫ5Θ®…α»ΞΘ©Θ§¥Υ ±DΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Ήέ…œΥυ ωΘ§Β±ΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ© ±Θ§÷±œΏBCΑ―ΓςBDFΖ÷≥…ΟφΜΐ÷°±»ΈΣ2ΘΚ3ΒΡΝΫ≤ΩΖ÷ΘΜ
Θ© ±Θ§÷±œΏBCΑ―ΓςBDFΖ÷≥…ΟφΜΐ÷°±»ΈΣ2ΘΚ3ΒΡΝΫ≤ΩΖ÷ΘΜ
Θ®3Θ©≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ÷±œΏxΘΫ2Θ§»γΆΦΘ§
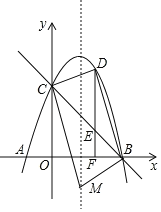
…ηMΘ®2Θ§tΘ©Θ§
ΓΏBΘ®5Θ§0Θ©Θ§CΘ®0Θ§5Θ©Θ§
ΓύBC2ΘΫ52+52ΘΫ50Θ§MC2ΘΫ22+Θ®t©¹5Θ©2ΘΫt2©¹10t+29Θ§MB2ΘΫΘ®2©¹5Θ©2+t2ΘΫt2+9Θ§
Β±BC2+MC2ΘΫMB2 ±Θ§ΓςBCMΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœBCMΘΫ90ΓψΘ§Φ¥50+t2©¹10t+29ΘΫt2+9Θ§ΫβΒΟtΘΫ7Θ§¥Υ ±MΒψΒΡΉχ±ξΈΣΘ®2Θ§7Θ©ΘΜ
Β±BC2+MB2ΘΫMC2 ±Θ§ΓςBCMΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœCBMΘΫ90ΓψΘ§Φ¥50+t2+9ΘΫt2©¹10t+29Θ§ΫβΒΟtΘΫ©¹3Θ§¥Υ ±MΒψΒΡΉχ±ξΈΣΘ®2Θ§©¹3Θ©ΘΜ
Β±MC2+MB2ΘΫBC2 ±Θ§ΓςBCMΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœCMBΘΫ90ΓψΘ§Φ¥t2©¹10t+29+t2+9ΘΫ50Θ§ΫβΒΟt1ΘΫ6Θ§t2ΘΫ©¹1Θ§¥Υ ±MΒψΒΡΉχ±ξΈΣΘ®2Θ§6Θ©ΜρΘ®2Θ§©¹1Θ©Θ§
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡMΒψΒΡΉχ±ξΈΣΘ®2Θ§7Θ©Θ§Θ®2Θ§©¹3Θ©Θ§Θ®2Θ§6Θ©Θ§Θ®2Θ§©¹1Θ©Θ°


 ΟΩΩΈ±ΊΝΖœΒΝ–¥πΑΗ
ΟΩΩΈ±ΊΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–3’≈ΤΥΩΥ≈ΤΘ§Ζ÷±π «ΚλΧ“3ΓΔΚλΧ“4ΚΆΚΎΧ“5Θ°Α―≈Τœ¥‘»ΚσΦΉœ»≥ι»Γ“Μ’≈Θ§Φ«œ¬Μ®…ΪΚΆ ΐΉ÷ΚσΫΪ≈ΤΖ≈ΜΊΘ§œ¥‘»Κσ““‘Ό≥ι»Γ“Μ’≈Θ°
Θ®1Θ©œ»ΚσΝΫ¥Έ≥ιΒΟΒΡ ΐΉ÷Ζ÷±πΦ«ΈΣxΚΆyΘ§Μ≠≥ω ς–ΈΆΦΜρΝ–±μ«σ|x©¹y|Γί1ΒΡΗ≈¬ Θ°
Θ®2Θ©ΦΉΓΔ““ΝΫ»ΥΉω”ΈœΖΘ§œ÷”–ΝΫ÷÷ΖΫΑΗΘ°AΖΫΑΗΘΚ»τΝΫ¥Έ≥ιΒΟœύΆ§Μ®…Ϊ‘ρΦΉ ΛΘ§Ζώ‘ρ““ ΛΘ°BΖΫΑΗΘΚ»τΝΫ¥Έ≥ιΒΟ ΐΉ÷ΚΆΈΣΤφ ΐ‘ρΦΉ ΛΘ§Ζώ‘ρ““ ΛΘ°«κΈ ΦΉ―Γ‘ώΡΡ÷÷ΖΫΑΗ Λ¬ ΗϋΗΏΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
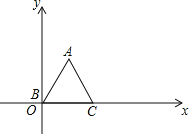
ΓΨΧβΡΩΓΩ“―÷ΣΒ»±ΏΓςABCΘ§ΕΞΒψBΘ®0Θ§0Θ©Θ§CΘ®2Θ§0Θ©Θ§ΙφΕ®Α―ΓςABCœ»―Ίx÷α»ΤΉ≈ΒψCΥ≥ ±’κ–ΐΉΣΘ§ ΙΒψA¬δ‘Ύx÷α…œΘ§≥ΤΈΣ“Μ¥Έ±δΜΜΘ§‘Ό―Ίx÷α»ΤΉ≈ΒψAΥ≥ ±’κ–ΐΉΣΘ§ ΙΒψB¬δ‘Ύx÷α…œΘ§≥ΤΈΣΕΰ¥Έ±δΜΜΘ§Γ≠Ψ≠ΙΐΝ§–χ2018¥Έ±δΜΜΚσΘ§ΕΞΒψAΒΡΉχ±ξ «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΪ«ζœΏyΘΫ![]() Θ®xΘΨ0Θ©Ψ≠ΙΐΓςOABΒΡΕΞΒψAΚΆOBΒΡ÷–ΒψCΘ§ABΓΈx÷αΘ§ΒψAΒΡΉχ±ξΈΣΘ®2Θ§3Θ©Θ§BEΓΆx÷αΘ§¥ΙΉψΈΣEΘ°
Θ®xΘΨ0Θ©Ψ≠ΙΐΓςOABΒΡΕΞΒψAΚΆOBΒΡ÷–ΒψCΘ§ABΓΈx÷αΘ§ΒψAΒΡΉχ±ξΈΣΘ®2Θ§3Θ©Θ§BEΓΆx÷αΘ§¥ΙΉψΈΣEΘ°

Θ®1Θ©»ΖΕ®kΒΡ÷ΒΘΚΓΓ ΓΓΘΜ
Θ®2Θ©ΦΤΥψΓςOABΒΡΟφΜΐΘΜ
Θ®3Θ©»τΒψDΘ®3Θ§bΘ©‘ΎΥΪ«ζœΏyΘΫ![]() Θ®xΘΨ0Θ©…œΘ§÷±œΏADΒΡΫβΈω ΫΈΣyΘΫmx+nΘ§«κ÷±Ϋ”–¥≥ω≤ΜΒ» Ϋmx+nΘΦ
Θ®xΘΨ0Θ©…œΘ§÷±œΏADΒΡΫβΈω ΫΈΣyΘΫmx+nΘ§«κ÷±Ϋ”–¥≥ω≤ΜΒ» Ϋmx+nΘΦ![]() ΒΡΫβΦ·ΘΚΓΓ ΓΓΘ°
ΒΡΫβΦ·ΘΚΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
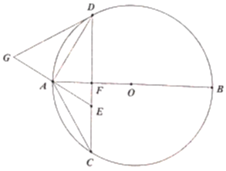
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§DCΈΣΓ―OΒΡ«–œΏΘ§DEΓΆABΘ§¥ΙΉψΈΣΒψEΘ§ΫΜΓ―O”ΎΒψFΘ§œ“ACΫΜDE”ΎΒψPΘ§Ν§Ϋ”CFΘ°
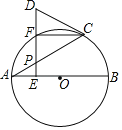
Θ®1Θ©«σ÷ΛΘΚΓœDPCΘΫΓœPCDΘΜ
Θ®2Θ©»τAPΘΫ2Θ§ΧνΩ’ΘΚ
ΔΌΒ±ΓœCABΘΫΓΓ ΓΓ ±Θ§ΥΡ±Ώ–ΈOBCF «Νβ–ΈΘΜ
ΔΎΒ±ACΘΫ2AE ±Θ§OBΘΫΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§Ε‘Ϋ«œΏACΘ§BDœύΫΜ”ΎΒψOΘ°
Θ®1Θ©Μ≠≥ωΓςAOBΤΫ“ΤΚσΒΡ»ΐΫ«–ΈΘ§ΤδΤΫ“ΤΚσΒΡΖΫœρΈΣ…δœΏADΒΡΖΫœρΘ§ΤΫ“ΤΒΡΨύάκΈΣADΒΡ≥ΛΘ°
Θ®2Θ©Ιέ≤λΤΫ“ΤΚσΒΡΆΦ–ΈΘ§≥ΐΝΥΨΊ–ΈABCDΆβΘ§ΜΙ”–“Μ÷÷ΧΊ βΒΡΤΫ––ΥΡ±Ώ–ΈΘΩ«κ÷ΛΟςΡψΒΡΫα¬έΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ±Ώ…œ“ΜΕ·ΒψΘ®Βψ
±Ώ…œ“ΜΕ·ΒψΘ®Βψ![]() ”κΒψ
”κΒψ![]() ≤Μ÷ΊΚœΘ©Θ§ΝΣΫα
≤Μ÷ΊΚœΘ©Θ§ΝΣΫα![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ±Ώ
ΫΜ±Ώ![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
Θ®1Θ©»γΆΦΘ§Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
Θ®2Θ©…η![]() Θ§«σ
Θ§«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΫβΈω Ϋ≤Δ–¥≥ωΚ· ΐΕ®“ε”ρΘΜ
ΒΡΚ· ΐΫβΈω Ϋ≤Δ–¥≥ωΚ· ΐΕ®“ε”ρΘΜ
Θ®3Θ©Α―![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() Ζ≠’έΒΟ
Ζ≠’έΒΟ![]() Θ§ΝΣΫα
Θ§ΝΣΫα![]() Θ§Β±
Θ§Β±![]() «Β»―ϋ»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ω
«Β»―ϋ»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ω![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§÷±ΨΕ
÷–Θ§÷±ΨΕ![]() ¥Ι÷±”Ύ≤ΜΙΐ‘≤–Ρ
¥Ι÷±”Ύ≤ΜΙΐ‘≤–Ρ![]() ΒΡœ“
ΒΡœ“![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§«“
…œΘ§«“![]() .ΙΐΒψ
.ΙΐΒψ![]() Ής
Ής![]() ΒΡ«–œΏΫΜ
ΒΡ«–œΏΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣ
ΈΣ![]() …œ“ΜΕ·ΒψΘ§…ηœΏΕΈ
…œ“ΜΕ·ΒψΘ§…ηœΏΕΈ![]() ΒΡ≥ΛΈΣ
ΒΡ≥ΛΈΣ![]() .
.
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©…η![]() ΑκΨΕΈΣ
ΑκΨΕΈΣ![]() Θ§»τΒψ
Θ§»τΒψ![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§«σ
÷–ΒψΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦΔΌΘ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§ΓςAEFΒΡΕΞΒψEΘ§FΖ÷±π‘ΎBCΘ§CD±Ώ…œΘ§ΗΏAG”κ’ΐΖΫ–ΈΒΡ±Ώ≥ΛœύΒ»Θ§«σΓœEAFΒΡΕ» ΐΘ°
Θ®2Θ©»γΆΦΔΎΘ§‘ΎRtΓςABD÷–Θ§ΓœBAD=90ΓψΘ§AB=ADΘ§ΒψMΘ§N «BD±Ώ…œΒΡ»Έ“βΝΫΒψΘ§«“ΓœMAN=45ΓψΘ§ΫΪΓςABM»ΤΒψAΡφ ±’κ–ΐΉΣ90Γψ÷ΝΓςADHΈΜ÷ΟΘ§Ν§Ϋ”NHΘ§ ‘≈–ΕœMN2Θ§ND2Θ§DH2÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
Θ®3Θ©‘ΎΆΦΔΌ÷–Θ§»τEG=4Θ§GF=6Θ§«σ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com