Question

顺次连接对角线相等的四边形各边中点，所得四边形是

1. A.
   矩形
2. B.
   平行四边形
3. C.
   菱形
4. D.
   任意四边形

Answer 1

C
分析：顺次连接对角线相等的四边形各边中点，所得四边形是菱形，理由为：根据题意画出四边形ABCD，E，F，G，H分别为各边的中点，写出已知，求证，由E，H分别为AB，AD的中点，得到EH为三角形ABD的中位线，根据三角形的中位线定理得到EH平行于BD，且等于BD的一半，同理FG平行于BD，且等于BD的一半，可得出EH与FG平行且相等，根据一组对边平行且相等的四边形为平行四边形得出EFGH为平行四边形，再由EF为三角形ABC的中位线，得出EF等于AC的一半，由EH等于BD的一半，且AC=BD，可得出EH=EF，根据邻边相等的平行四边形为菱形可得证．
解答：顺次连接对角线相等的四边形各边中点，所得四边形是菱形，
如图所示：

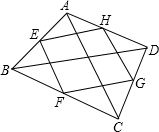
已知：E，F，G，H分别为四边形ABCD各边的中点，且AC=BD，
求证：四边形EFGH为菱形，
证明：∵E，F，G，H分别为四边形ABCD各边的中点，
∴EH为△ABD的中位线，FG为△CBD的中位线，
∴EH∥BD，EH=BD，FG∥BD，FG=BD，
∴EH∥FG，EH=FG=BD，
∴四边形EFGH为平行四边形，
又EF为△ABC的中位线，
∴EF=AC，又EH=BD，且AC=BD，
∴EF=EH，
∴四边形EFGH为菱形．
故选C
点评：此题考查了三角形的中位线定理，平行四边形的判定，以及菱形的判定，利用了数形结合及等量代换的思想，灵活运用三角形中位线定理是解本题的关键．