
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

【答案】(1)MN=AM+BN成立,理由见解析;(2)MN=BNAM,理由见解析.
【解析】
(1)利用同角的余角相等证明∠MAC=∠NCB,由∠AMC=∠CNB=90°,AC=BC,可证△AMC≌△CNB,从而有AM=CN,MC=BN,即可得出结论;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
解:(1)MN=AM+BN成立;
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,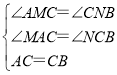 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=CN+MC,
∴MN=AM+BN;
(2)MN=BNAM.
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,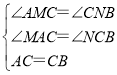 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=MCCN,
∴MN=BNAM.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米):
+6 | - 5 | +9 | - 10 | +13 | - 9 | - 4. |
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共走了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双边直尺有两条平行的边,但是没有刻度,可以用来画等距平行线:
![]()
我们也可用工具自制(如图):
![]()
下面是小My同学设计的“过直线外一点作这条直线的平行线”的双边直尺作图过程.
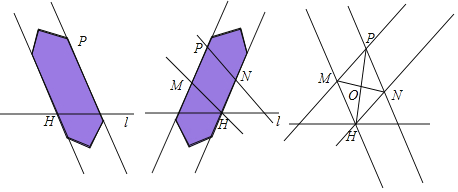
(1)根据小My同学的作图过程,请证明O为PH中点.
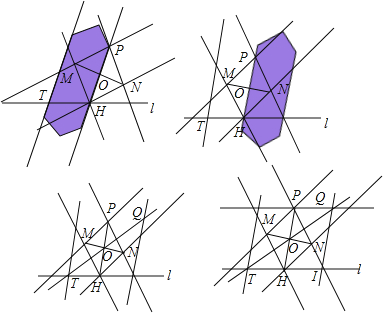
(2)根据小My同学的作图过程,请证明PQ∥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点A、C分别在
的顶点A、C分别在![]() 、
、![]() 的正半轴上,反比例函数
的正半轴上,反比例函数![]() (
(![]() )与矩形
)与矩形![]() 的边AB、BC交于点D、E.
的边AB、BC交于点D、E.

(1)若![]() ,则
,则![]() 的面积为_________;
的面积为_________;
(2)若D为AB边中点.
①求证:E为BC边中点;
②若![]() 的面积为4,求
的面积为4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com