
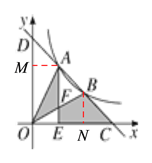
【题目】如图,一次函数y=-x+b与反比例函数y=![]() (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(1)b=________(用含m的代数式表示);
(2)若S△OAF+S四边形EFBC=4,则m的值是________.

【答案】 m+![]()
![]()
【解析】(1)∵点A在函数![]() 的图象上,且A的横坐标为
的图象上,且A的横坐标为![]() ,
,
∴点A的纵坐标为![]() ,
,
又∵点A在一次函数![]() 的图象上,
的图象上,
∴![]() ,解得
,解得![]() ;
;
(2)如下图,过点A作AM⊥OD于点M,过点B作BN⊥OC于点N,
∵函数![]() 与
与![]() 的图象都关于直线
的图象都关于直线![]() 对称,
对称,
∴AM=BN=OE,△DOA≌△COB,
设△OAF的面积为![]() ,∵S△OAE =2,S△OAF+S四边形EFBC=4,
,∵S△OAE =2,S△OAF+S四边形EFBC=4,
∴S△OEF=S△OAE- ![]() =
= ![]() ,S四边形EFBC =
,S四边形EFBC = ![]() ,
,
∴S△DOA=S△COB=S△OEF+ S四边形EFBC =![]() ,
,
∴S△ADM= S△DOA - S△OAM =![]() ,
,
∴S△ADM =2 S△OEF,
又∵OE=MA,
∴EF=![]() AM=
AM=![]() BN,
BN,
由EF∥BN可知△OEF∽△OBN,∴ ![]()
∴点E是ON的中点,
∴ON=2OE=2AM=![]() ,
,
∴点B的坐标为![]() ,
,
把B的坐标代入![]() 得:
得: ![]() ,解得
,解得![]() ,
,
又∵![]() ,
,
∴![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】某市建设地铁2号线,有一项工程原计划由甲工程队独立完成需要20天.在甲工程队施工4天后,为了加快工程进度,又调来乙工程队与甲工程队共同施工,结果比原计划提前10天完成任务.求:
⑴ 乙工程队独立完成这项工程需要的时间;
⑵ 甲、乙两工程队分别完成这项工程工作量的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 和双曲线
和双曲线![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com