
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
【答案】(1)见解析;(2)见解析
【解析】
试题(1)根据题意画出图形即可;
(2)首先根据等腰三角形的性质与三角形内角与外角的性质证明∠ACB=∠FAC,进而可得AF∥BC;然后再根据线段的垂直平分线的性质可知:OA=OC, ∠AOF=∠COE=90°,AE=EC,FA=FC,由OA=OC, ∠AOF=∠COE=90°,∠CAM=∠ACB可证明AOF≌△COE,即可得到AF=EC.因此可由AF∥BC,AF=EC,得证四边形AECF是平行四边形.最后可由AC⊥EF得证结论:菱形.
试题解析:(1)

(2)猜想:四边形AECF是菱形
证明:∵AB=AC ,AM平分∠CAD
∴∠B=∠ACB,∠CAD=2∠CAM
∵∠CAD是△ABC的外角
∴∠CAD=∠B+∠ACB
∴∠CAD=2∠ACB
∴∠CAM=∠ACB
∴AF∥CE
∵EF垂直平分AC
∴OA=OC, ∠AOF=∠COE=![]()
∴AOF≌△COE
∴AF=CE
在四边形AECF中,AF∥CE,AF=CE
∴四边形AECF是平行四边形
又∵EF⊥AC
∴四边形AECF是菱形


科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
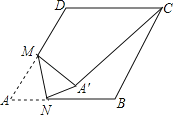
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是![]() ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
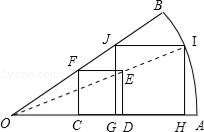
【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com