
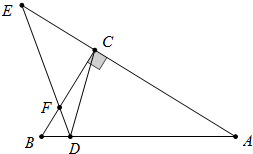
 △ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.
△ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4. 分析 作CM⊥AB于M,CN∥DE交AB于N.首先证明BF=BD=1,设CF=DN=x,AN=y,则AC=x+y,在Rt△ABC利用勾股定理推出x2=2y,由CN∥DE,得$\frac{AC}{CE}$=$\frac{AN}{DN}$,得$\frac{x+y}{EC}$=$\frac{y}{x}$,得EC=$\frac{{x}^{2}+xy}{y}$=2+x,在Rt△EFC中,由EF2=EC2+CF2,可得x2+(2+x)2=(2$\sqrt{5}$)2,解方程即可解决问题.
解答 解:如图,作CM⊥AB于M,CN∥DE交AB于N.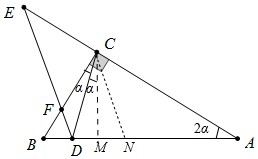
∵∠ACB=∠AMC=90°,
∴∠ACM+∠A=90°,∠B+∠A=90°,
∴∠ACM=∠B,同理∠A=∠BCM,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ACM+∠DCM=∠B+∠BCD,
∴∠DCB=∠DCM,设∠DCB=∠DCM=α,则∠BCM=∠A=2α,
∵∠BFD=∠EDC+α=45°+α,∠B=90°-2α,
∴∠BDF=180°-∠B-∠BFD=45°+α,
∴∠BFD=∠BDF,
∴BF=BD=1,
∵DF∥CN,
∴∠BCN=∠BFD,∠BNC=∠BDF,
∴∠BCN=∠BNC,
∴BC=DN,设BC=DN=x,AN=y,则AC=x+y,
在Rt△ABC中,∵BC2+AC2=AB2,
∴(1+x)2+(x+y)2=(1+x+y)2,
∴x2=2y,
∵CN∥DE,
∴$\frac{AC}{CE}$=$\frac{AN}{DN}$,
∴$\frac{x+y}{EC}$=$\frac{y}{x}$,
∴EC=$\frac{{x}^{2}+xy}{y}$=2+x,
在Rt△EFC中,∵EF2=EC2+CF2,
∴x2+(2+x)2=(2$\sqrt{5}$)2,
∴x=2,y=2,
∴AD=x+y=4.
故答案为4.
点评 本题考查等腰三角形的性质和判定、勾股定理、平行线分线段成比例定理等知识,解题的关键是学会利用参数解决问题,学会添加常用辅助线,题目比较难,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 两人都对 | B. | 两人都不对 | C. | 甲对、乙不对 | D. | 甲不对,乙对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -24÷22=-4 | B. | -22÷(-32)=$\frac{4}{27}$ | C. | -2×$\frac{1}{{3}^{2}}$=-8$\frac{1}{27}$ | D. | (-1)2016=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com