
分析 (1)首先化简二次根式进而合并求出答案;
(2)首先化简二次根式进而合并求出答案;
(1)直接利用绝对值的性质以及二次根式的性质、负整数指数幂的性质、零指数幂的性质分别化简求出答案;
(2)利用乘法公式化简二次根式进而合并求出答案.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{3}$+3$\sqrt{5}$
=$\sqrt{3}$+3$\sqrt{5}$;
(2)原式=$\frac{\sqrt{2}}{2}$+4$\sqrt{2}$-2×$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$-5$\sqrt{3}$
=$\frac{17\sqrt{2}}{4}$-$\frac{17\sqrt{3}}{3}$;
(3)原式=$\sqrt{2}$-1+1-3+2
=$\sqrt{2}$-1;
(4)原式=3+1-2$\sqrt{3}$-(3-2)
=4-2$\sqrt{3}$-1
=3-2$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算以及绝对值的性质,正确化简二次根式是解题关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3x}{2}$ | B. | $\frac{4}{x-y}$ | C. | $\frac{{{x^2}+1}}{π}$ | D. | $\frac{x-y}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $-\frac{4}{9}$ | C. | $\frac{4}{9}$ | D. | $-\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
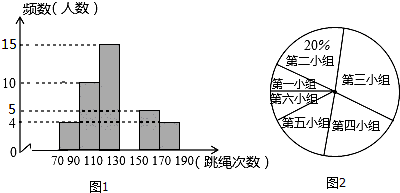
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com