

分析 (1)设抛物线的解析式为y=a(x-3)(x+1),将点C的坐标代入求得a的值,然后利用配方法可求得抛物线的顶点坐标;
(2)当点N在DE上时.过点P作PF⊥OB,垂足为F.先证明△NEB≌△BFP,于是得到BE=PF=2,设点P的坐标为(x,x2-2x-3).由PF=2列出关于x的方程可求得点P的坐标;当点M在ED上时,过点P作PG⊥OB,垂足为G,过点P作PF⊥ED,垂足为F.先证明△PMF≌△PBG,设点P的坐标为(x,x2-2x-3).然后依据PG=PF列出关于x的方程,从而可求得点P的坐标;
(3)连接BC,过点C作CH⊥DE于H,分别延长QC、DC,与x轴相交于点P,R.先证明△BCD∽△QOC,由相似三角形的性质可得到点P的坐标,然后再求得直线CP与直线BD的解析式,然后可求得两直线的交点坐标即可.
解答 解:(1)设抛物线的解析式为y=a(x-3)(x+1).
∵将点C的坐标代入得:-3a=-3,解得:a=1,
∴抛物线的解析式为y=x2-2x-3.
∴y=(x-1)2-4.
∴抛物线的顶点D的坐标为(1,-4).
(2)如图1所示:当点N在DE上时.过点P作PF⊥OB,垂足为F.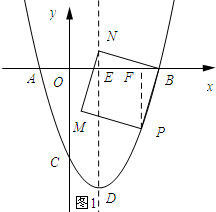
∵BPMN为正方形,
∴∠NBE+∠PBF=90°.
又∵∠PBF+∠FPB=90°,
∴∠NBE=∠FPB.
在△NEB和△BFP中$\left\{\begin{array}{l}{∠NBE=∠FPB}\\{∠NEB=∠BFP=90°}\\{NB=PB}\end{array}\right.$,
∴△NEB≌△BFP.
∴BE=PF=2.
设点P的坐标为(x,x2-2x-3).则-x2+2x+3=2整理得:x2-2x-1=0,
解得:x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$(舍去).
∴点P的坐标为(1+$\sqrt{2}$,-2).
当点M在ED上时,如图2所示:过点P作PG⊥OB,垂足为G,过点P作PF⊥ED,垂足为F.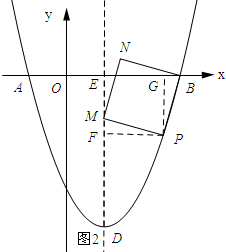
同理△PMF≌△PBG.
∴PG=PF.
设点P的坐标为(x,x2-2x-3).则-x2+2x+3=x-1.整理得:x2-x-4=0,
解得:x1=$\frac{1+\sqrt{17}}{2}$,x2=$\frac{1-\sqrt{17}}{2}$(舍去).
∴点P纵坐标=-(x-1)=1-$\frac{1+\sqrt{17}}{2}$=$\frac{1-\sqrt{17}}{2}$.
∴点P的坐标为($\frac{1+\sqrt{17}}{2}$,$\frac{1-\sqrt{17}}{2}$).
综上所述,点P的坐标为(1+$\sqrt{2}$,-2)或($\frac{1+\sqrt{17}}{2}$,$\frac{1-\sqrt{17}}{2}$).
(3)如图3所示:连接BC,过点C作CH⊥DE于H,分别延长QC、DC,与x轴相交于点P,R.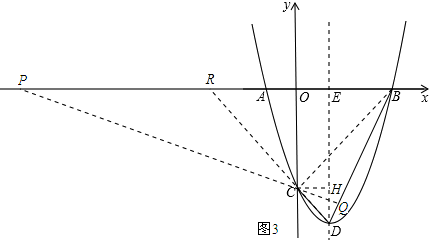
∵对称轴为直线x=1,
∴点E的坐标为(1,0)H点坐标为(1,-3).
∴CH=DH=1,
∴∠CDH=∠BCO=∠BCH=45°,
∴CD=$\sqrt{2}$,CB=3$\sqrt{2}$,△BCD为直角三角形.
∵∠BDE=∠DCQ=∠PCR,
∠CDB=∠CDE+∠BDE=45°+∠DCQ,
∠PCO=∠RCO+∠PCR=45°+∠DCQ,
∴∠CDB=∠PCO,
∴△BCD∽△QOC,
∴$\frac{PC}{OP}=\frac{CD}{CB}$=$\frac{1}{3}$,
∴OP=3OC=9,即P(-9,0).
∴直线CP的解析式为y=-$\frac{1}{3}$x-3,
设直线BD的解析式为y=kx+b.
∵将点B和点D的坐标代入得:$\left\{\begin{array}{l}{3k+b=0}\\{k+b=-4}\end{array}\right.$,解得:k=2,b=-6.
∴直线BD的解析式为y=2x-6.
由方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x-3}\\{y=2x-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{9}{7}}\\{y=-\frac{24}{7}}\end{array}\right.$.
∴点Q的坐标为($\frac{9}{7}$,-$\frac{24}{7}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、全等三角形的性质和判定、相似三角形的性质,证得△BCD∽△QOC,从而得到P的坐标是解题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
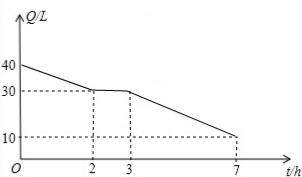
 如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物需要多长时间达到最大浓度?
如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物需要多长时间达到最大浓度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com