
 =m,由于当x≤1时y随x的增大而减小,则直线x=1在直线x=m的左侧,于是可对②进行判断;配方得到y=(x-m)2-m2-3,则抛物线向左平移3个单位的解析式为y=(x-m+3)2-m2-3,把原点坐标代入计算出m的值,则可对③进行判断;根据抛物线的对称性由当x=4时的函数值与x=2时的函数值相等得到抛物线的对称轴为直线x=3,则m=3,所以抛物线解析式为y=x2-6x-3,然后计算x=6时的函数值,则可对④进行判断.
=m,由于当x≤1时y随x的增大而减小,则直线x=1在直线x=m的左侧,于是可对②进行判断;配方得到y=(x-m)2-m2-3,则抛物线向左平移3个单位的解析式为y=(x-m+3)2-m2-3,把原点坐标代入计算出m的值,则可对③进行判断;根据抛物线的对称性由当x=4时的函数值与x=2时的函数值相等得到抛物线的对称轴为直线x=3,则m=3,所以抛物线解析式为y=x2-6x-3,然后计算x=6时的函数值,则可对④进行判断. =m,当在对称轴左侧时,y随x的增大而减小,而当x≤1时y随x的增大而减小,∴m≥1,所以②错误;
=m,当在对称轴左侧时,y随x的增大而减小,而当x≤1时y随x的增大而减小,∴m≥1,所以②错误; ,抛物线顶点坐标为(-
,抛物线顶点坐标为(-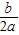 ,
, );抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
);抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点. 

 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
 (2012•镇江)对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
(2012•镇江)对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com