
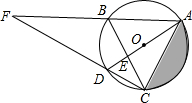
 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:分析 (1)由圆周角定理可知:∠ADC=∠ABC=60°,从而可求出∠ECD=40°,所以∠AEC=∠ECD+∠ADC=100°,再求出∠FAC=∠DAC+∠BAD=70°,从而可知∠AFC=90°-∠FAC=20°.
(2)连接CO,作OH⊥AC于点H,分别求出△AOC与扇形AOC的面积,从而可求出阴影部分面积.
解答 解:(1)由圆周角定理可知:∠ADC=∠ABC=60°,
∵AD是⊙O的直径,
∴∠DCA=90°,
∴∠ECD=∠DCA-∠ACB=40°,
∴∠AEC=∠ECD+∠ADC=100°,
由圆周角定理可知:∠BAD=∠ECD=40°,
∵∠DAC=180°-∠AEC-∠ACB=30°,
∴∠FAC=∠DAC+∠BAD=70°,
∴∠AFC=90°-∠FAC=20°,
(2)连接CO,作OH⊥AC于点H,
则∠AOC=2∠ABC=120°,
∠DAC=30°,
∴OH=$\frac{1}{2}$OA=$\frac{3}{2}$
AC=3$\sqrt{3}$
∴S△AOC=$\frac{1}{2}$AC•OH=$\frac{1}{2}$×3$\sqrt{3}$×$\frac{3}{2}$=$\frac{9\sqrt{3}}{4}$
S阴影=S扇形-S△AOC
=$\frac{120π×9}{360}$--$\frac{9\sqrt{3}}{4}$
=3π-$\frac{9\sqrt{3}}{4}$
故答案为:(1)100°;20°
点评 本题考查圆的综合问题,涉及圆周角定理,三角形内角和定理,扇形面积公式等知识,综合程度较高,属于中等题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
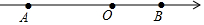 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com