
【题目】如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( ) 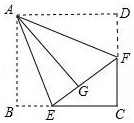
A.1.5
B.2.5
C.2.25
D.3
【答案】B
【解析】解:∵正方形纸片ABCD的边长为3, ∴∠C=90°,BC=CD=3,
根据折叠的性质得:EG=BE=1,GF=DF,
设DF=x,
则EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2,
∵在Rt△EFC中,EF2=EC2+FC2 , 即(x+1)2=22+(3﹣x)2 , 解得:x=1.5,
∴DF=1.5,EF=1+1.5=2.5.
故选B.
由正方形纸片ABCD的边长为3,可得∠C=90°,BC=CD=3,由根据折叠的性质得:EG=BE=1,GF=DF,然后设DF=x,在Rt△EFC中,由勾股定理EF2=EC2+FC2 , 即可得方程,解方程即可求得答案.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 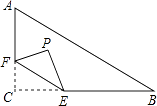
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校从初二(1)班和(2)班各选拔10名同学组成甲队和乙队,参加数学竞赛活动,此次竞赛共有10道选择题,答对8题(含8题)以上为优秀,两队选手答对题数统计如下:
答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数( |
甲队选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 |
乙队选手 | 0 | 0 | 4 | 3 | 2 | 1 | a |
中位数 | 众数 | 方差(s2) | 优秀率 | ||||
甲队选手 | 8 | 8 | 1.6 | 80% | |||
乙队选手 | b | c | 1.0 | m | |||
(1)上述表格中,a= ,b= ,c= ,m= .
(2)请根据平均数和众数的意义,对甲、乙两队选手进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 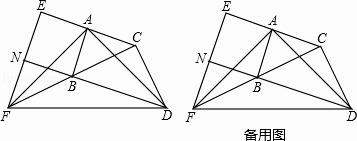
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 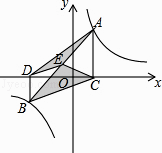
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=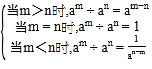
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:![]() = ,43÷45= .
= ,43÷45= .
(2)如果 3x-1÷33x-4=![]() ,求出 x 的值.
,求出 x 的值.
(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com