
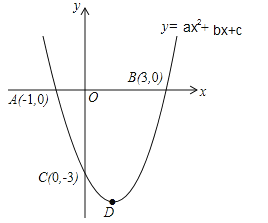
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴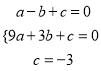 ,解得:
,解得: 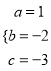 ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() );
);
②当DA=DP时, ![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当AD=AP时, ![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
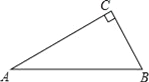
【题目】如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
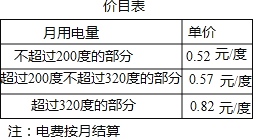
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250﹣200)=132.5元.
(1)若某户居民10月份电费78元,则该户居民10月份用电_______度;
(2)若该户居民2月份用电340度,则应缴电费_______元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com