
【题目】如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.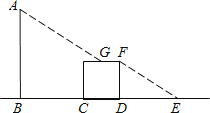
A.8
B.7
C.6
D.5
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.
(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20厘米,那么相邻一条边的边长等于厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要测量旗杆高CD , 在B处立标杆AB=2.5cm,人在F处.眼睛E、标杆顶A、旗杆顶C在一条直线上.已知BD=3.6m,FB=2.2m,EF=1.5m.求旗杆的高度.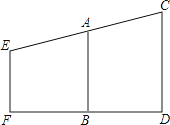
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,∠BAD的平分线交BD于点E , 交CD于点F , 交BC的延长线于点G , 则下列结论中正确的是( ) 
A.AE2=EFFG
B.AE2=EFEG
C.AE2=EGFG
D.AE2=EFAG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正△ABC中,D、E分别在AC、AB上,且 ![]() =
= ![]() , AE=BE , 则有( )
, AE=BE , 则有( ) 
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65 岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化.从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果.所谓“老年人口抚养比”是指某范围人口中,老年人口数(65 岁及以上人口数)与劳动年龄人口数(15﹣64 岁人口数)之比,通常用百分比表示,用以表明每100 名劳动年龄人口要负担多少名老年人.
以下是根据我国近几年的人口相关数据制作的统计图和统计表.
2011﹣2014 年全国人口年龄分布图
2011﹣2014 年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0﹣14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15﹣64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
根据以上材料解答下列问题:
(1)2011 年末,我国总人口约为亿,全国人口年龄分布表中m的值为;
(2)若按目前我国的人口自然增长率推测,到2027 年末我国约有14.60 亿人.假设0﹣14岁人口占总人口的百分比一直稳定在16.5%,15﹣64岁人口一直稳定在10 亿,那么2027 年末我国0﹣14岁人口约为亿,“老年人口抚养比”约为;(精确到1%)
(3)2016 年1 月1 日起我国开始实施“全面二胎”政策,一对夫妻可生育两个孩子,在未来10年内,假设出生率显著提高,这(填“会”或“不会”)对我国的“老年人口抚养比”产生影响.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com