
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题解析:如图,
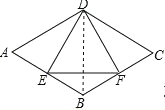
连接BD,
∵四边形ABCD是菱形,
∴AD=AB, ![]() ,AB∥CD,
,AB∥CD,
∵∠A=60°,
∴∠ADC=120°,∠ADB=60°,
同理:∠DBF=60°,
即∠A=∠DBF,
∴△ABD是等边三角形,
∴AD=BD,
∵∠ADE+∠BDE=60°,∠BDE+∠BDF=∠EDF=60°,
∴∠ADE=∠BDF,
∵在△ADE和△BDF中, ![]() ,
,
∴△ADE≌△BDF(ASA),
∴DE=DF,AE=BF,故①正确;
∵∠EDF=60°,
∴△EDF是等边三角形,
∴②正确;
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠AED+∠ADE=180°-∠A=120°,
∴∠ADE=∠BEF;
故④正确.
∵△ADE≌△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF.
故③错误.
综上所述,结论正确的个数为3个.故本题应选C.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
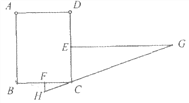
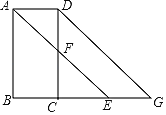
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
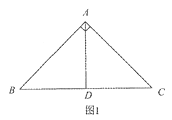
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
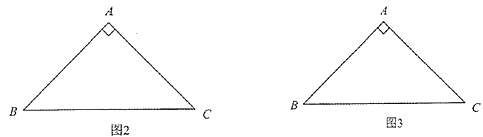
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名同学调查了全班![]() 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 | 划记 | 人数 | 百分数(%) |
相声 | 正 |
|
|
小品 | 正正正一 |
|
|
歌曲 | 正正 |
|
|
舞蹈 | 正一 |
|
|
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量分别为45人/辆和30人/辆和租金分比为400元/辆和280元/辆:杏坛中学根据实际情况,计划租用A,B型客车共5辆,同时送八年级师生到基地参加社会实践活动,若要保证租车费用不超过1900元,求A型客车的数量最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com