
在平面直角坐标系xOy中,一次函数y=- x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)求点P的坐标(用含t的代数式表示);
(2)当点Q从点O向点B运动时(未到达点B),是否存在实数t,使得△BPQ的面积大于17若存在,请求出t的取值范围;若不存在,请说明理由;
(3)伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.是否存在t的值,使得直线l经过点O?若存在,请求出所有t的值;若不存在,请说明理由.
(1)P(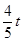 ,﹣
,﹣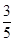 x+3);
x+3);
(2)不存在实数t,使得△BPQ的面积大于17;
(3),t=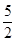 或
或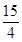 时,O在l的垂直平分线上.
时,O在l的垂直平分线上.
解析试题分析:(1)表示边长首要就是表示出来,根据函数性质及线段成比例等性质易表示出,PD,PC的长,即得坐标;
(2)讨论面积一般是计算底和高,然后表示出面积解析式,进而根据二次函数性质讨论最值或范围.而第一问求得OA=3,OB=4,易得S△AOB仅为6,而S△BQP≤S△AOB,所以定不存在实数t,使得面积大于17;
(3)垂直平分线上的点到两边距离相等,利用这个性质,我们只要表示出OP,和OQ即可.但讨论时注意Q点的运动时个往返的过程,要有两种情形.
试题解析:(1)如图,过点P作PC⊥OA于C,PD⊥OB于D.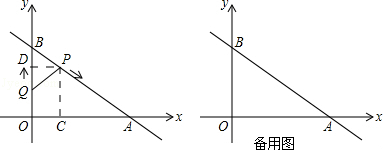
∵y=﹣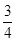 x+3的图象与x轴交于点A,与y轴交于点B
x+3的图象与x轴交于点A,与y轴交于点B
∴A(4,0),B(0,3),
在Rt△BDP中,
∵OB=3,OA=4,
∴AB=5.
∵BP∥OA,
∴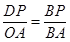 ,
,
∵BP=t,
∴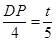 ,
,
∴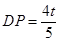 .
.
∵由点P过AB,
∴将x=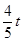 代入y=﹣
代入y=﹣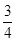 x+3,得y=﹣
x+3,得y=﹣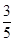 x+3,
x+3,
∴P(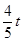 ,﹣
,﹣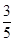 x+3);
x+3);
(2)不存在实数t,使得△BPQ的面积大于17.
∵Q、P在OB、OA上运动,
∴S△BQP≤S△AOB.
∵S△AOB= OA·OB=
OA·OB=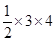 =6,
=6,
∴S△BQP≤6<17,
∴不存在实数t,使得△BPQ的面积大于17;
(3)∵P(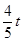 ,﹣
,﹣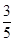 x+3),
x+3),
∴OC=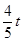 ,PC=﹣
,PC=﹣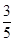 x+3,
x+3,
∴OP2=(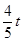 )2+(﹣
)2+(﹣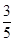 x+3)2,
x+3)2,
∵O在l的垂直平分线上,
∴OP=OQ.
①当0<t≤3时,OP=t,则t2=(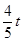 )2+(﹣
)2+(﹣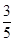 t+3)2,解得 t=
t+3)2,解得 t=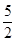 ,符合要求.
,符合要求.
②当3<t≤5时,
∵BQ=t﹣3,
∴OQ=3﹣(t﹣3)=6﹣t,
∴(6﹣t)2=(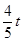 )2+(﹣
)2+(﹣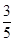 t+3)2
t+3)2
解得 t=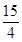 ,符合要求.
,符合要求.
综上所述,t=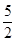 或
或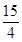 时,O在l的垂直平分线上.
时,O在l的垂直平分线上.
考点:一次函数综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
无论k取任何实数,对于直线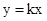 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线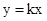 恒过定点
恒过定点 .
.
(1)无论 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了抓住世界杯商机,某商店决定购进A、B两种世界杯纪念品.若购进A种纪念品10件,B种纪念品5件,需要1 000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,
①根据信息填表:
| | A地 | B地 | C地 | 合计 |
| 产品件数(件) | x | | 2x | 200 |
| 运费(元) | 30x | | | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,A(1,0),B(4,0),M(5,3).动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求l的解析式;
(2)若l与线段BM有公共点,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在y轴上.如不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com