
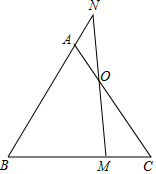
 如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.
如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON. 分析 过M作ME∥BN交AC于点E.首先证明△EMC是等边三角形,再证明△NAO≌△MEO即可.
解答 证明:过M作ME∥BN交AC于点E.
∵△ABC是等边三角形,
∴AB=AC,∠C=60°,
∴∠B=∠EMC=∠C,
∴EM=EC,
∴△EMC是等边三角形,
∴EM=MC,
∵AN=MC
∴AN=ME,
∵AN∥ME
∴∠ANO=∠EMO,∠NAO=∠MEO
在△NAO和△MEO中,
$\left\{\begin{array}{l}{∠N=∠OME}\\{AN=EM}\\{∠NAO=∠OEM}\end{array}\right.$,
∴△NAO≌△MEO,
∴OM=ON.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
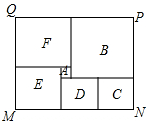 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,点P(6,0),以P为圆心,10为半径的圆分别交坐标轴于点A、B、C、D.
如图,平面直角坐标系中,点P(6,0),以P为圆心,10为半径的圆分别交坐标轴于点A、B、C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com