
 一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)
一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)分析 根据题意,可以得到∠ABD和∠ACD的度数,由于AB=20,从而可以求得BD、AD、CD的长,从而可以求得该船航行的速度.
解答 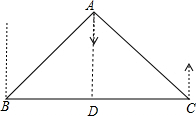 解:作AD⊥BC于点D,如右图所示,
解:作AD⊥BC于点D,如右图所示,
由已知可得,∠ADB=90°,∠ABD=90°-37°=53°,AB=20,
∴BD=AB•cos53°=20×0.6=12,AD=AB•sin53°=20×0.8=16,
又∵∠ADC=90°,∠ACD=90°-50°=40°,AD=16,
∴CD=$\frac{AD}{tan40°}=\frac{16}{0.84}$≈19.05
∴该船航行的速度是:(12+19.05)÷1.5=20.7海里/小时,
即该船航行的速度是20.7海里/小时.
点评 本题考查解直角三角形的应用-方向角问题,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
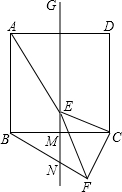 已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N
已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
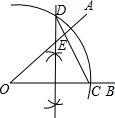 如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.
如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com