
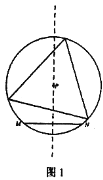
����Ŀ�����壺��ͼl��ʾ�������߶�MN���䴹ֱƽ������һ��P�����Ե�PΪԲ�ģ�PMΪ�뾶���Ż������Բ����MN�ϴ��������������Ϊһ���ȱ������εĶ��㣬��Ƶ�PΪ�߶�MN�ġ�����㡱���ر�ģ��������ĵȱ�������ֻ����һ������Ƶ�PΪ�߶�MN�ġ�ǿ����㡱��
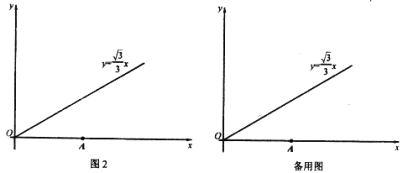
���⣺��ͼ2��ʾ��ƽ��ֱ������ϵxOy�У���A������Ϊ��2![]() ��0������B������y=
��0������B������y=![]() x��x��0���ϡ�
x��x��0���ϡ�
��1���ڵ�C��![]() ��0����D��
��0����D��![]() ��1����E��
��1����E��![]() ��-2���У����Գ�Ϊ�߶�OA�ġ�����㡱����__________.
��-2���У����Գ�Ϊ�߶�OA�ġ�����㡱����__________.
��2������һ�����ڴ���һ��Q�����߶�OA�ġ�����㡱�������߶�OB�ġ�ǿ����㡱�����B�����ꡣ
��3���ڣ�2���������£��Ե�AΪԲ�ģ�ABΪ�뾶��Բ�������Բ��x�ύ�����Ҳ�һ��ΪH��Բ��һ����K��H��������A˳ʱ����ת180���ֹͣ�����K������ת���ĽǶ�Ϊ![]() ��0��<
��0��< ![]() ��180�㣩�����߶�OB��AK�����ڹ���������㡱����ֱ��д��
��180�㣩�����߶�OB��AK�����ڹ���������㡱����ֱ��д��![]() ��ȡֵ��Χ��_______________��
��ȡֵ��Χ��_______________��
���𰸡���1��D��E��
��2��B��3![]() ��3����
��3����
��3��30��< ![]() <90���
<90���![]() =150�㡣
=150�㡣
�����������������(1)���ų����ж�;(2) �������֪Q���Ϊ�߶�OA������������������߶�OB����ǿ������������Q��������OA��OB�Ĵ�ֱƽ�����ϣ��ҡ�QOB=30����
y=![]() x��x��ļн�Ϊ30�������QOA=60�������Q������Ϊ(m,n)��Q����OA�Ĵ�ֱƽ�����ϣ���m=
x��x��ļн�Ϊ30�������QOA=60�������Q������Ϊ(m,n)��Q����OA�Ĵ�ֱƽ�����ϣ���m=![]() ��
�� ![]() ��QB=QO=
��QB=QO=![]() ������B(
������B(![]() ��
��
(3)���Բ���ù�O��Q�㣬F������Ϊ��![]() ��0��������������Ҫ����������ζ�����120�ȣ�ͨ����ͼ�������a�ķ�ΧΪ��30�� <a<90������a=150������ʱAK���д�����OB���д���ƽ�У�û�н�������߶�OB�������������AE������QF�ϣ����߶�AK�������Ҫ�������������н�����
��0��������������Ҫ����������ζ�����120�ȣ�ͨ����ͼ�������a�ķ�ΧΪ��30�� <a<90������a=150������ʱAK���д�����OB���д���ƽ�У�û�н�������߶�OB�������������AE������QF�ϣ����߶�AK�������Ҫ�������������н�����
���������
��1��D��E��
��2����Q�����߶�OA������������������߶�OB����ǿ���������
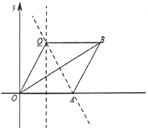
�����֪����OQB=120������QOB=30������QOA=60����
��Q��![]() ��3��.
��3��.
OQ=BQ=2![]() ��BQ��OA��
��BQ��OA��
��B��3![]() ��3��.
��3��.
��3�������֪��
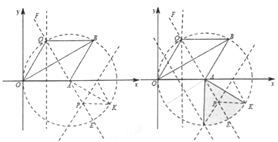
�߶�OB�������������AE������QF�ϣ�
���߶�AK�������Ҫ�������������н��㣬
��0< ![]() ��30����90���
��30����90���![]() <150����150��<
<150����150��< ![]() ��180�����ڽ��㡣
��180�����ڽ��㡣
���������ڣ���30��< ![]() <90����
<90����![]() =150��.
=150��.
�㾦:������������,��Ҫ���������¸���,�ܽ�ͷ����¹���,Ȼ��ͨ��ģ��,��Ȼ���ɽ������,�ؼ�������������������ӱ�Ľ��ⷽ��,Ȼ������ת��˼����ݱ������Ͻ�Ҫ�������ת��Ϊ�Ķ������ķ������������.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
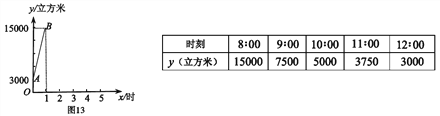
����Ŀ��Ϊ��Լ��Դ��ij���ڶ����Ӧ���٣���ȼ��������װΪ��Ȼ������.ij������7:00��8:00�� ȼ����˾���ó�������վ�Ĵ���������8:00 ����վ��ʼΪǰ���ij�������. �������ڵ���Ȼ������y�������ף������ʱ��x��ʱ���ı仯���仯.
��1����7:00��8:00 ��Χ�ڣ�y ��x�ı仯�����ͼ13 ��ʾ����y ����x �ĺ�������ʽ��
��2����8:00��12:00 ��Χ�ڣ�y �ı仯������±���ʾ����д��һ�����ϱ��������ݵ�y ����x �ĺ�������ʽ�����˺�������ʽ���ж�����9��05 ��9��20 �ܷ���ɼ���950 ����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��C��E��ͬһ��ֱ���ϣ���ABC���CDE���ǵȱ������Σ������н��۲�һ���������ǣ� �� 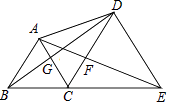
A.��ACE�ա�BCD
B.��BGC�ա�AFC
C.��ADB�ա�CEA
D.��DCG�ա�ECF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ�ǡ�ABC�У���ACB=90�㣬AC=BC��DΪAB�е㣬DE��DF�� 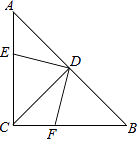
��1��д��ͼ������ȫ�������Σ��ֱ�Ϊ �� ���á��ա����ű�ʾ��
��2����֤��ED=DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB=12cm����E��AB�ϣ���AE= ![]() AB���ӳ��߶�AB����C��ʹBC=
AB���ӳ��߶�AB����C��ʹBC= ![]() AB����D��BC���е㣬���߶�DE�ij���
AB����D��BC���е㣬���߶�DE�ij���![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ͼ����������ijһֱ�߷����ƶ�����õ�һ���µ�ͼ�Σ������ƶ��ͽ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷ���x2��8x��7��0����Ϊ(x��h)2��k����ʽӦΪ
A.(x��4)2����7B.(x��4)2����7C.(x��4)2��9D.(x��4)2��9
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com