
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2 ![]() ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( ) 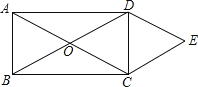
A.2 ![]()
B.4
C.4 ![]()
D.8
【答案】A
【解析】解:连接OE,与DC交于点F,
∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD,即OA=OB=OC=OD,
∵OD∥CE,OC∥DE,
∴四边形ODEC为平行四边形,
∵OD=OC,
∴四边形ODEC为菱形,
∴DF=CF,OF=EF,DC⊥OE,
∵DE∥OA,且DE=OA,
∴四边形ADEO为平行四边形,
∵AD=2 ![]() ,DE=2,∴OE=2
,DE=2,∴OE=2 ![]() ,即OF=EF=
,即OF=EF= ![]() ,在Rt△DEF中,
,在Rt△DEF中,
根据勾股定理得:DF= ![]() =1,即DC=2,则S菱形ODEC=
=1,即DC=2,则S菱形ODEC= ![]() OEDC=
OEDC= ![]() ×2
×2 ![]() ×2=2
×2=2 ![]() .
.
故选A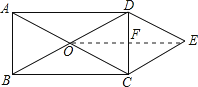
连接OE,与DC交于点F,由四边形ABCD为矩形得到对角线互相平分且相等,进而得到OD=OC,再由两组对边分别平行的四边形为平行四边形得到ODEC为平行四边形,根据邻边相等的平行四边形为菱形得到四边形ODEC为菱形,得到对角线互相平分且垂直,求出菱形OCEF的面积即可.此题考查了矩形的性质,菱形的判定与性质,以及勾股定理,熟练掌握矩形的性质是解本题的关键.


科目:初中数学 来源: 题型:
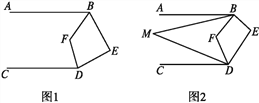
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1、用不超过16800元购进A、B两类图书共1000本; | |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.
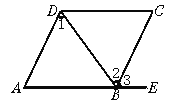
(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.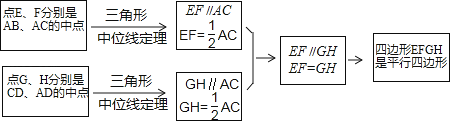
结合小敏的思路作答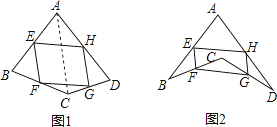
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.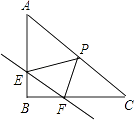
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com