
 如图,⊙O的半径为1,圆心O在正三角形的边AB的中点,⊙O向顶点A方向运动,O到A点终止,若AB=10,运动速度为1个单位/秒,运动时间设为t.试问:
如图,⊙O的半径为1,圆心O在正三角形的边AB的中点,⊙O向顶点A方向运动,O到A点终止,若AB=10,运动速度为1个单位/秒,运动时间设为t.试问:分析 利用AC与⊙O相切于点D,△ABC为正三角形,可求得sin∠A=$\frac{OD}{OA}$,利用特殊角的三角函数值可求得OA的值,根据直线和圆的位置关系解答即可.
解答 解:当AC与⊙O相切于点D时,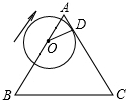 ∠ADO=90°,
∠ADO=90°,
∵△ABC为正三角形,
∴∠A=60°.
∴sin∠A=$\frac{OD}{OA}$,
OA=$\frac{2\sqrt{3}}{3}$,
(1)当0≤t<5-$\frac{2\sqrt{3}}{3}$时,⊙O与直线AC相离;
(2)当t=5-$\frac{2\sqrt{3}}{3}$时,⊙O与直线AC相切;
(3)当5-$\frac{2\sqrt{3}}{3}$<t≤5时,⊙O与直线AC相交.
点评 本题考查了圆的切线的性质及三角函数的定义的应用,直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交?d<r,②直线l和⊙O相切?d=r,③直线l和⊙O相离?d>r,解题时要注意数形结合思想的运用.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
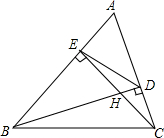 如图,△ABC中,高BD、CE相交于点H,求证:
如图,△ABC中,高BD、CE相交于点H,求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com