
分析 根据加减消元法,可得方程组的解.
解答 解:(1)原方程组可化简为$\left\{\begin{array}{l}{4x-y=5①}\\{3x+2y=12②}\end{array}\right.$,
①×2+②得
11x=22,
解得x=2,
把x=2代入①,得8-y=5,
解得y=3,
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
(2)原方程组化简为$\left\{\begin{array}{l}{2x-17y=24①}\\{3x+2y=146②}\end{array}\right.$,
②×2-①×3,得
55y=220,
解得y=4
把y=4代入①,得
2x-68=24,
解得x=46
原方程组的解为$\left\{\begin{array}{l}{x=46}\\{y=4}\end{array}\right.$.
点评 本题考查了解二元一次方程组,利用等式的性质化简方程组是解题关键,又利用了加减消元法.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
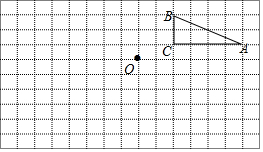 如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C,O都在格点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C,O都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
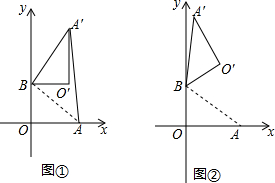
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
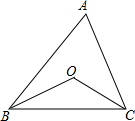 如图,已知点O是△ABC的两条角平分线的交点,
如图,已知点O是△ABC的两条角平分线的交点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
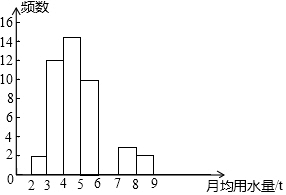 小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 0.04 |
| 3≤x<4 | 12 | 0.24 |
| 4≤x<5 | 15 | 0.3 |
| 5≤x<6 | 10 | 0.2 |
| 6≤x<7 | 6 | 0.12 |
| 7≤x<8 | 3 | 0.06 |
| 8≤x<9 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
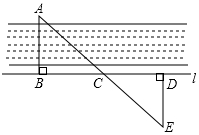 如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com