
【题目】如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动. 
(1)当E与F不重合时,四边形DEBF是否是平行四边形?请说明理由;
(2)若AC=16cm,BD=12cm,点E,F在运动过程中,四边形DEBF能否为矩形?如能,求出此时的运动时间t的值,如不能,请说明理由.
【答案】
(1)解:当E与F不重合时,四边形DEBF是平行四边形
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD;
∵E、F两动点,分别从A、C两点以相同的速度向C、A运动,
∴AE=CF;
∴OE=OF;
∴BD、EF互相平分;
∴四边形DEBF是平行四边形
(2)解:∵四边形DEBF是平行四边形,
∴当BD=EF时,四边形DEBF是矩形;
∵BD=12cm,
∴EF=12cm;
∴OE=OF=6cm;
∵AC=16cm;
∴OA=OC=8cm;
∴AE=2cm或AE=14cm;
由于动点的速度都是1cm/s,
所以t=2(s)或t=14(s);
故当运动时间t=2s或14s时,以D、E、B、F为顶点的四边形是矩形.
【解析】(1)判断四边形DEBF是否为平行四边形,需证明其对角线是否互相平分;已知了四边形ABCD是平行四边形,故OB=OD;而E、F速度相同,方向相反,故OE=OF;由此可证得BD、EF互相平分,即四边形DEBF是平行四边形;(2)若以D、E、B、F为顶点的四边形是矩形,则必有BD=EF,可据此求出时间t的值.
【考点精析】掌握平行四边形的判定与性质和矩形的判定方法是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,△ABE时等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 . 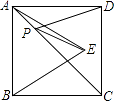
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种长方体集装箱,其内空长为5米,集装箱截面的高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,为了尽可能多运,排的方案是:圆柱长5米放置于集装箱内空长,圆柱两底面放置于集装箱截面,截面的排法是:
A. 横排,每行分别为4、3、4、3、4、3
B. 横排,每行分别为4、4、4、4、4、3
C. 竖排,每列分别为5、4、5、4、5
D. 竖排,每列分别为5、5、5、5、4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=8,将矩形沿AC折叠,点D落在点F处,AF与BC交于点E. 
(1)判断△AEC的形状,并说明理由;
(2)求△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:

(1)∵________=__________(已知)
∴AB∥CD(同位角相等,两条直线平行)
(2)∵_________=__________(已知)
∴AB∥CD(内位角相等,两条直线平行)
(3)∵_________+_________=180(已知)
∴AB∥CD(同旁内角互补,两条直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com