练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．若一次函数y=（m-3）x+5的函数值，y随x的增大而增大，则（　　）
    A．m＜0B．m＞0C．m＜3D．m＞3

    分析 直接根据一次函数的性质可得m-3＞0，解不等式即可确定答案．

    解答 解：∵一次函数y=（m-3）x+5中，y随着x的增大而增大，
    ∴m-3＞0，
    解得：m＞3．
    故选：D

    点评 本题考查的是一次函数的性质，熟知一次函数y=kx+b（k≠0）中，当k＜0时，y随x的增大而减小是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费，分两档收费：第一档是当月用电量不超过240度时实行“基础电价”；第二档是当用电量超过240度时，其中的240度仍按照“基础电价”计费，超过的部分按照“提高电价”收费．设每个家庭月用电量为x度时，应交电费为y元．具体收费情况如折线图所示，请根据图象回答下列问题：
    （1）“基础电价”是0.5元/度；
    （2）求出当x＞240时，y与x的函数表达式；
    （3）小石家六月份缴纳电费132元，求小石家这个月用电量为多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．问题再现：
    如图1：△ABC中，AF为BC边上的中线，则S△ABF=S△ACP=$\frac{1}{2}$S△ABC
    由这个结论解答下列问题：
    问题解决：
    问题1：如图2，△ABC中，CD为AB边上的中线，BE为AC边上的中线，则S△BOC=S四边形ADOE．
     分析：△ABC中，CD为AB边上的中线，则S△BCD=$\frac{1}{2}$S△ABC，BE为AC边上的中线，则S△ABE=$\frac{1}{2}$S△ABC
    ∴S△BCD=S△ABE
    ∴S△BCD-S△BOD=S△ABE-S△BOD
    又∵S△BOC=S△BCD-S△BOD，S四边形ADOE=S△ABE-S△BOD
    即S△BOC=S四边形ADOE
    问题2：如图3，△ABC中，CD为AB边上的中线，BE为AC边上的中线，AF为BC边上的中线．
    （1）S△BOD=S△COE吗？请说明理由．
    （2）请直接写出△BOD的面积与△ABC的面积之间的数量关系：S△BOD=$\frac{1}{6}$S△ABC．
    问题拓广：
    （1）如图4，E、F分别为四边形ABCD的边AD、BC的中点，请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系：S阴=$\frac{1}{2}$S四边形ABCD．
    （2）如图5，E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点，请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系：S阴=$\frac{1}{3}$S四边形ABCD．
    （3）如图6，E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点，
    若S△AME=1、S△BNG=1.5、S△CQF=2、S△BFH△DFH=2.5，则S阴=7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，每个小正方形的边长为1，△ABC的三个顶点都在格点（小正方形的顶点）上．
    （1）己知A（-3，2）．建立平面直角坐标系并写出B、C的坐标；
    （2）将△ABC先向右平移6个单位，再向上平移3个单位得△A1B1C1，画出平移后的△A1B1C1；
    （3）若以A、B、C、D为顶点的四边形为平行四边形，直接写出D点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

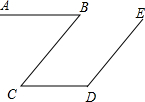    3．已知：如图所示，AB∥CD，∠B+∠D=180°．求证：BC∥DE
    证明：∵AB∥CD  已知
    ∴∠B=∠C（两直线平行，内错角相等）
    ∵∠B+∠D=180°已知
    ∴∠C+∠D=180°  （等量代换）
    ∴BC∥DE（同旁内角互补，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．能够成为直角三角形边长的三个正整数，我们称之为一组勾股数，观察表格所给出的三个数a，b，c，a＜b＜c．
    （1）试找出它们的共同点，并证明你的结论；
    （2）写出当a=17时，b，c的值．
    3，4，5　　32+42=52
    　5，12，13，　52+122=132
    　7，24，25　72+242=252
    　9，40，41　92+402=412
    ……
    　17，b，c　172+b2=c2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．完成证明，说明理由．已知：如图，BC∥DE，点E在AB边上，DE、AC交于点F，∠1=∠2，∠3=∠4，求证AE∥CD．
    证明：∵BC∥DE（已知），
    ∴∠4=∠FCB（两直线平行，同位角相等）．
    ∵∠3=∠4（已知），
    ∴∠3=∠FCB（等量代换）．
    ∵∠1=∠2（已知），
    ∴∠1+∠FCE=∠2+∠FCE（等式的性质）．
    即∠FCB=∠ECB，
    ∴∠3=∠ECD（等量代换）．
    ∴AE∥CD（内错角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知一个等腰三角形的两边长分别为$\sqrt{18}$和$\sqrt{50}$，则这个等腰三角形的周长为（　　）
    A．11$\sqrt{2}$B．13$\sqrt{2}$C．11$\sqrt{3}$或$\sqrt{3}$D．11$\sqrt{2}$或13$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知点P（m，n）在第四象限，那么点Q（n-1，-m）在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案