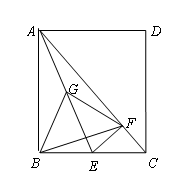
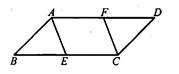
试题分析:(1)通过角的转换和等腰直角三角形的性质,得到∠BAE=∠CAF和∠B=∠FCA,从而ASA证明△ABF≌△ACF,根据全等三角形对应边相等得到结论.
(2)①过E点作EG⊥AB于点G,通过证明EG是BM的垂直平分线就易得出结论.
②通过证明Rt△AMC≌Rt△EMC和△ADE≌△CDN来证明结论.
试题解析:(1)如图,∵∠BAC=90°,FA⊥AE,∴∠1+∠EAC=90°,∠2+∠EAC=90°.
∴∠1=∠2.
又∵AB=AC,∴∠B=∠ACB=45°.
∵FC⊥BC,∴∠FCA=90°-∠ACB=45°.∴∠B=∠FCA.
∴△ABF≌△ACF(ASA).∴BE=CF.
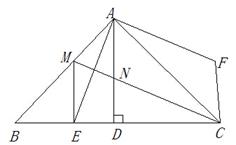
(2)①如图,过E点作EG⊥AB于点G,
∵∠B=45°,∴△CBE是等腰直角三角形.∴BG=EG,∠3=45°.
∵BM=2DE,∴BM=2BG,即点G是BM的中点.∴EG是BM的垂直平分线.∴∠4=∠3=45°.
∴∠MEB=∠4+∠3=90°.∴ME⊥BC.
②∵AD⊥BC,∴ME∥AD.∴∠5=∠6.
∵∠1=∠5,∴∠1=∠6.∴AM=EM.
∵MC=MC,∴Rt△AMC≌Rt△EMC(HL).∴∠7=∠8.
∵∠BAC=90°,,AB=AC,∴∠ACB=45°,∠BAD=∠CAD=45°.
∴∠5=∠7=22.5°,AD=CD.
∵∠ADE=∠CDN=90°,∴△ADE≌△CDN(ASA).∴DE=DN.





 阅读快车系列答案
阅读快车系列答案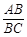 =k.
=k.