
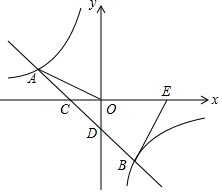
 如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于点C,与y轴交于点D,点E是x轴正半轴上一点,若OC=2,点E的坐标为(4,0),点B的纵坐标为-4,且tan∠OEB=2.
如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于点C,与y轴交于点D,点E是x轴正半轴上一点,若OC=2,点E的坐标为(4,0),点B的纵坐标为-4,且tan∠OEB=2.分析 (1)过B作BF⊥x轴于F,由B的纵坐标为-4,tan∠OEB=2,求得FE=2,即可求得B(2,-4),根据C(-2,0),B(2,-4)用待定系数法及可求得结论;
(2)求出D点坐标,再解方程组$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=-x-2}\end{array}\right.$,求出A点坐标,根据三角形面积公式即可求得结论.
解答  解(1)过B作BF⊥x轴于F,
解(1)过B作BF⊥x轴于F,
∵B的纵坐标为-4,且tan∠OEB=2,
∴FE=2,
∵点E的坐标为(4,0),
∴F(2,0),
∴B(2,-4),
∴m=2×(-4)=-8,反比例函数的解析式为y=-$\frac{8}{x}$,把C(-2,0),
∴B(2,-4)代入y=kx+b得:$\left\{\begin{array}{l}{-2k+b=0}\\{2k+b=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-2}\\{k=-1}\end{array}\right.$
一次函数函数的解析式为y=-x-2;
(2)y=-x-2,当x=0,解得:y=-2,
∴D(0,-2),解方程组$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=-x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=-4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{y}_{2}=2}\end{array}\right.$,
∴A(-4,2),
∴A到x轴的距离是4,
∴△AOD的面积=$\frac{1}{2}$×2×4=4.
点评 此题考查了待定系数法求函数解析式,反比例函数与一次函数的交点问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
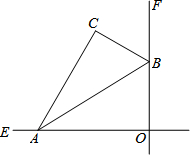 如图,直线OE与直线OF互相垂直,将含30°的三角尺ABC如图摆放,其斜边两端点A、B分别落在OE、OF上,且AB=12cm
如图,直线OE与直线OF互相垂直,将含30°的三角尺ABC如图摆放,其斜边两端点A、B分别落在OE、OF上,且AB=12cm查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3>|-3| | B. | -6>5 | C. | -0.2>0.02 | D. | -$\frac{1}{5}$<-$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
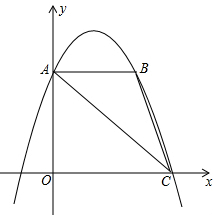 如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.
如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我国民众对“乐天萨德事件”的看法 | |
| B. | 了解浙江卫视“奔跑吧兄弟”节目的收视率 | |
| C. | 调查我校某班学生喜欢上数学课的情况 | |
| D. | 调查某类烟花爆竹燃放的安全情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
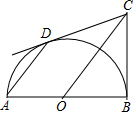 如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.
如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com