
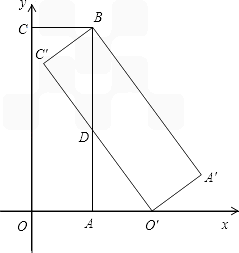
解:(1)连接BO和BO',由题意知OA=O'A,
∴点O'的坐标为(2,0);
(2)设AD=m,
∵BC'=O'A=1,∠BC'D=∠O'AD=90°,∠BDC'=∠O'DA,
∴Rt△BDC' Rt△O'DA,
Rt△O'DA,
∴C'D=AD=m,则DO'=3﹣m;
在Rt△ADO'中,AD2+AO'2=DO'2,
∴m2+12=(3﹣m)2,解之得:m= ,
,
∴线段AD的长度为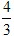 ;
;
(3)设经过点O'、C'的直线的函数表达式为:y=kx+b,
由(1)和(2)得点O'的坐标为(2,0),点D的坐标为(1, ),
),
而点O'和D都在这条直线上,
∴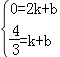 ,解之得:k=﹣
,解之得:k=﹣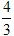 ,b=
,b= .
.
∴经过点O'、C'的直线的函数表达式为:y=﹣ x+
x+ .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
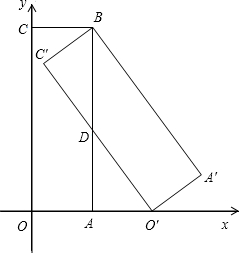 (1,0)、(0,3),现将矩形ABCO绕点B逆时针旋转得矩形A′BC′O′,使点O′落在x轴的正半轴上,且AB与C′O′交于点D,求:
(1,0)、(0,3),现将矩形ABCO绕点B逆时针旋转得矩形A′BC′O′,使点O′落在x轴的正半轴上,且AB与C′O′交于点D,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1,0)、(0,3),现将矩形ABCO绕点B逆时针旋转得矩形A′BC′O′,使点O′落在x轴的正半轴上,且AB与C′O′交于点D,求:
(1,0)、(0,3),现将矩形ABCO绕点B逆时针旋转得矩形A′BC′O′,使点O′落在x轴的正半轴上,且AB与C′O′交于点D,求:查看答案和解析>>
科目:初中数学 来源:湖北省期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:广东省期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com