
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为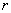 米,面积为
米,面积为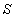 平方米.(注:
平方米.(注: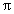 的近似值取3)
的近似值取3)
(1)求出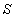 与
与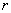 的函数关系式,并写出自变量
的函数关系式,并写出自变量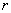 的取值范围;
的取值范围;
(2)当半径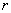 为何值时,扇形花坛的面积最大,并求面积的最大值.
为何值时,扇形花坛的面积最大,并求面积的最大值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
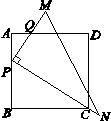
已知:如图,Rt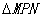 的顶点P在正方形ABCD的边AB上,∠MPN=90°,PN经过点C,PM与AD交于点Q.
的顶点P在正方形ABCD的边AB上,∠MPN=90°,PN经过点C,PM与AD交于点Q.
(1)在不添加字母和辅助线的情况下,图中△APQ∽△ ;
(2)若P为AB的中点,联结CQ,求证:AQ+BC=CQ;
(3)若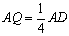 时,试探究线段PC与线段PQ的数量关系,并加以证明.
时,试探究线段PC与线段PQ的数量关系,并加以证明.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
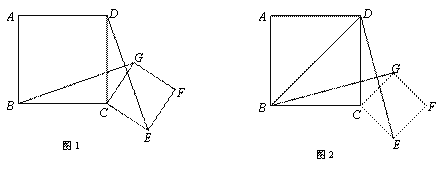
已知四边形ABCD和四边形CEFG都是正方形 ,且AB>CE.
(1)如图1,连接BG、DE.求证:BG=DE;
(2)如图2,如果正方形ABCD的边长为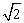 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得C
,将正方形CEFG绕着点C旋转到某一位置时恰好使得C G//BD,BG=BD.
G//BD,BG=BD.
①求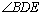 的度数;
的度数;
②请直接写出正方形CEFG的边长的值.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
一个袋子中装有10个球,其中有6个黑球和4个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机从这个袋子中摸出一个球,摸到黑球的概率为
A.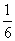 B.
B.
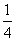 C.
C.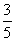 D.
D.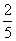

查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线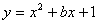 的顶点在x轴上,且与y轴交于A点. 直线
的顶点在x轴上,且与y轴交于A点. 直线 经过A、B两点,点B的坐标为(3,4).
经过A、B两点,点B的坐标为(3,4).
(1)求抛物线的解析式,并判断点B是否在抛物线上;
(2)如果点B在抛物线上,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h ,点P的横坐标为x.当x为何值时,h取得最大值,求出这时的h值.
查看答案和解析>>
科目:初中数学 来源: 题型:
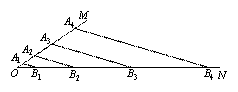
如图,点A1、A2 、A3 、…,点B1、B2 、B3 、…,分别在射线OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A 4=4OA1,….
那么A2B2= ,AnBn= .(n为正整数)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com