
 如图,点C为线段AB上一点,将线段CB绕点C旋转,得到线段CD,若DA⊥AB,AD=1,$BD=\sqrt{17}$,则BC的长为$\frac{17}{8}$.
如图,点C为线段AB上一点,将线段CB绕点C旋转,得到线段CD,若DA⊥AB,AD=1,$BD=\sqrt{17}$,则BC的长为$\frac{17}{8}$.  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
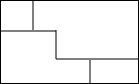 夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )
夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )| A. | 280m | B. | 140m | C. | 90m | D. | 70m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
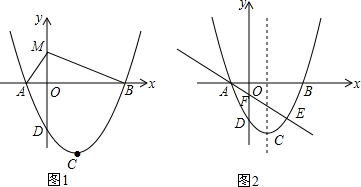
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com