
分析 (1)根据绝对值、零指数幂、特殊角的三角函数值可以解答本题;
(2)根据分式的减法和约分可以解答本题.
解答 解:(1)$\sqrt{4}$+|-2|-(-5)0-2sin30°
=2+2-1-2×$\frac{1}{2}$
=2+2-1-1
=2;
(2)$\frac{x+2}{{x}^{2}-4}$-$\frac{{x}^{2}-2x}{{x}^{2}-4x+4}$
=$\frac{x+2}{(x+2)(x-2)}-\frac{x(x-2)}{(x-2)^{2}}$
=$\frac{1}{x-2}-\frac{x}{x-2}$
=$\frac{1-x}{x-2}$.
点评 本题考查分式的混合运算、绝对值、零指数幂、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
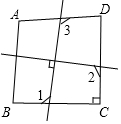 如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )| A. | ∠1=∠2>∠3 | B. | ∠1=∠3>∠2 | C. | ∠2>∠1=∠3 | D. | ∠3>∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
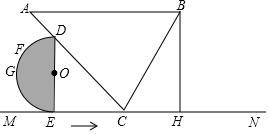 如图,∠A=45°,∠ABC=60°,AB∥MN,BH⊥MN于点H,BH=8,点C在MN上,点D在AC上,DE⊥MN于点E,半圆的圆心为点O,直径DE=6,G为$\widehat{DE}$的中点,F是$\widehat{DE}$上的动点.
如图,∠A=45°,∠ABC=60°,AB∥MN,BH⊥MN于点H,BH=8,点C在MN上,点D在AC上,DE⊥MN于点E,半圆的圆心为点O,直径DE=6,G为$\widehat{DE}$的中点,F是$\widehat{DE}$上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
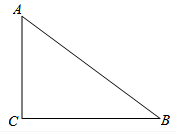 如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
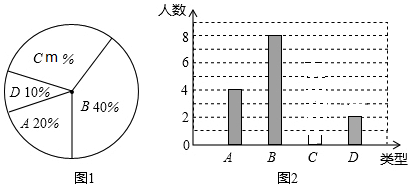
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+5)=150 | B. | x(x-5)=150 | C. | (x+5)(x-5)=150 | D. | (x+5)2=150 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com