
 如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$.
如图所示,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为$\frac{1}{{{2^{2012}}}}$. 分析 根据题意可知第2个正方形的边长是 $\frac{\sqrt{2}}{2}$×2,则第3个正方形的边长是( $\frac{\sqrt{2}}{2}$)2×2,…,进而可找出规律,第n个正方形的边长是( $\frac{\sqrt{2}}{2}$)n-1×2,那么易求S2015的值.
解答 解:根据题意:第一个正方形的边长为2;
第二个正方形的边长为:$\frac{\sqrt{2}}{2}$×2;
第三个正方形的边长为:( $\frac{\sqrt{2}}{2}$)2×2,
…
第n个正方形的边长是( $\frac{\sqrt{2}}{2}$)n-1×2,
所以S2015的值是( $\frac{1}{2}$)2012即$\frac{1}{{2}^{2012}}$.
故答案为$\frac{1}{{2}^{2012}}$.
点评 本题考查了正方形的性质、等腰直角三角形的性质、勾股定理.解题的关键是长特殊到一般,探究规律后,应用规律解决问题,属于中考常考题型.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
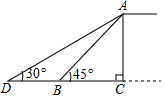 某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.
如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |
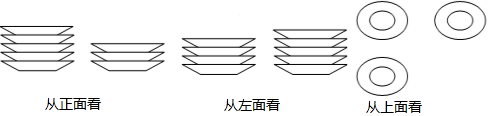
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com