
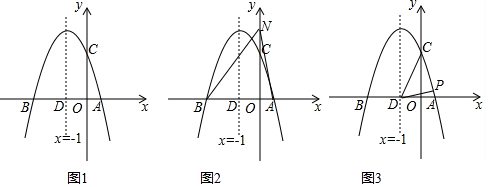
 如图,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
如图,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.分析 (1)利用待定系数法,把点A(4,-3)代入抛物线的解析式,即可解决问题.
(2)①求出PO、PH的长,即可解决问题.
②结论:PO=PH.设点P坐标(m,-$\frac{1}{4}$m2+1),利用两点之间距离公式求出PH、PO即可解决问题.
解答 (1)解:∵抛物线y=ax2+1经过点A(4,-3),
∴-3=16a+1,
∴a=-$\frac{1}{4}$,
∴抛物线解析式为y=-$\frac{1}{4}$x2+1,顶点B(0,1).
(2)①当P点运动到A点处时,∵PO=$\sqrt{{3}^{2}+{4}^{2}}$=5,PH=2-(-3)=5,
∴PO=PH,
故答案分别为5,5,=.
②结论:PO=PH.
理由:设点P坐标(m,-$\frac{1}{4}$m2+1),
∵PH=2-(-$\frac{1}{4}$m2+1)=$\frac{1}{4}$m2+1
PO=$\sqrt{{m}^{2}+(-\frac{1}{4}{m}^{2}+1)^{2}}$=$\sqrt{(\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}$m2+1,
∴PO=PH.
点评 本题考查二次函数综合题、待定系数法、点到直线的距离,两点间距离公式等知识,解题的关键是记住两点之间的距离公式,熟练掌握完全平方公式,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
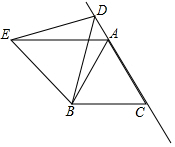 等边△ABC中,D是线段CA延长线上的点,以BD为一边作等边△EDB,连结AE.
等边△ABC中,D是线段CA延长线上的点,以BD为一边作等边△EDB,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com