
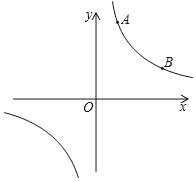
【题目】反比例函数![]() (k为常数,且k≠0)的图象经过点A(1,4)、(4,m).
(k为常数,且k≠0)的图象经过点A(1,4)、(4,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
【答案】(1)![]() ,B点坐标为(4,1);(2)P点坐标为(
,B点坐标为(4,1);(2)P点坐标为(![]() ,0).
,0).
【解析】
(1)先把A点坐标代入y=![]() 求出k得到反比例函数解析式;然后把B(4,m)代入反比例函数解析式求出m得到B点坐标;
求出k得到反比例函数解析式;然后把B(4,m)代入反比例函数解析式求出m得到B点坐标;
(2)作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,-4),利用两点之间线段最短可判断此时此时PA+PB的值最小,再利用待定系数法求出直线BA′的解析式,然后求出直线与x轴的交点坐标即可得到P点坐标.
(1)把A(1,4)代入y=![]() 得k=1×4=4,
得k=1×4=4,
∴反比例函数解析式为y=![]() ;
;
把B(4,m)代入y=![]() 得4m=4,解得m=1,
得4m=4,解得m=1,
∴B点坐标为(4,1);
(2)如图,作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,﹣4),

∵PA+PB=PA′+PB=BA′,
∴此时PA+PB的值最小,
设直线BA′的解析式为y=mx+n,
把A′(1,﹣4),B(4,1)代入得![]()
解得:
∴直线BA′的解析式为y=![]() ,
,
当y=0时,![]() =0,解得x=
=0,解得x=![]() ,
,
∴P点坐标为(![]() ,0).
,0).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C.

(1)求该抛物线的解析式;
(2)设该抛物线的顶点为D,求出△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家步行到校车站台,等候坐校车去学校,图中的折线表示这一过程中小明的路程S(km)与所花时间t(min)间的函数关系;下列说法:①他步行了1km到校车站台;②他步行的速度是100m/min;③他在校车站台等了6min;④校车运行的速度是200m/min;其中正确的个数是( )个.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数满足以下条件:①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);②对称轴是x=3;③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象中x>x2部分的图象向下翻折与原图象未翻折的部分组成图象“G”,试结合图象平行于x轴的直线y=m与图象“G”的交点的个数情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
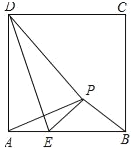
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为开展“大阅读”活动,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格少5元.已知学校用12000元购买的文学类图书的本数与用9000元购买的科普类图书的本数相等,求学校购买的科普图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
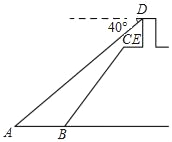
【题目】如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com