
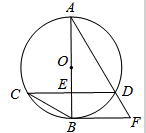
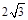 ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).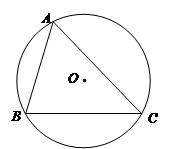
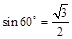 ,
,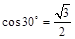 ,
,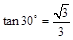 .)
.)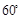 (2)
(2)

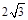 ,
, . ………………1分
. ………………1分 ,
, , ∴
, ∴ ,
,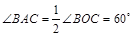 . ………………4分
. ………………4分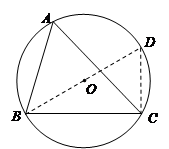
 .
. ,
, ,∴
,∴ .………………4分
.………………4分 .
. 在Rt△ABE中,∵
在Rt△ABE中,∵ ,
,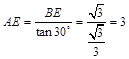 ,
, .
.  . ………………7分
. ………………7分 , ∴△ABC是等边三角形.
, ∴△ABC是等边三角形.  ,
,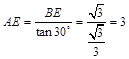 ,
, .
.  . ………………7分
. ………………7分 ,再利用圆周角的定理求得∠BAC的度数
,再利用圆周角的定理求得∠BAC的度数

 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
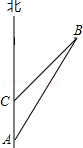
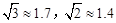 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
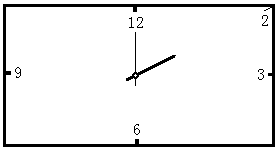
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com