
分析 由于∠AOC:∠COB=2:3,∠AOB=80°,可以求得∠AOC的度数,OD是角平分线,可以求得∠AOD的度数,∠COD=∠AOD-∠AOC.
解答 解:如图1,若OC在∠AOB内部,
∵∠AOC:∠COB=2:3,
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=80°,
∴2x+3x=80°,
得x=16°,
∴∠AOC=2x=2×16°=32°,∠COB=3x=3×16°=48°,
∵OD平分∠AOB,
∴∠AOD=40°,
∴∠COD=∠AOD-∠AOC=40°-32°=8°.
如图2,若OC在∠AOB外部,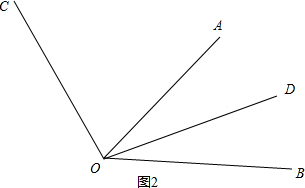
∵∠AOC:∠COB=2:3,
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=80°,
∴3x-2x=80°,
得x=80°,
∴∠AOC=2x=2×80°=160°,∠COB=3x=3×80°=240°,
∵∠AOC,∠COB均小于180°,
∴OC与∠AOB的平分线所成的角的度数为8°.
点评 本题考查了角的计算用到角平分线的性质,涉及到角的倍分关系时,一般通过设未知数,建立方程进行解决.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
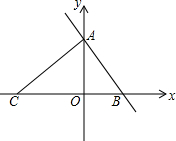 如图,在直角坐标系中,直线AB交y轴正半轴于点A(0,4),交x轴正半轴于点B,在x轴负半轴上有一点C,连接AC,△AOC的面积为12,△AOB的面积为4.
如图,在直角坐标系中,直线AB交y轴正半轴于点A(0,4),交x轴正半轴于点B,在x轴负半轴上有一点C,连接AC,△AOC的面积为12,△AOB的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
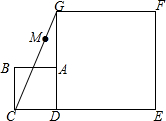 如图,四边形ABCD和四边形DEFG都是正方形.
如图,四边形ABCD和四边形DEFG都是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )
如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )| A. | 8 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com