
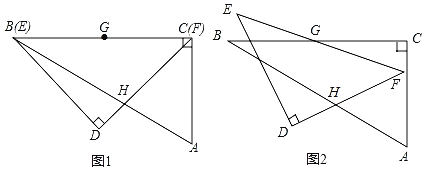
【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是_____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_____.(结果保留根号)
【答案】(12![]() ﹣12)cm (12
﹣12)cm (12![]() ﹣18)cm
﹣18)cm
【解析】
如图1中,作![]() 于
于![]() ,设
,设![]() .在
.在![]() 中,
中,![]() ,
,![]() ,根据
,根据![]() ,可得
,可得![]() ,推出
,推出![]() ,推出
,推出![]() .如图2中,当
.如图2中,当![]() 时,易证
时,易证![]() ,此时
,此时![]() 的值最小,易知
的值最小,易知![]() ,当旋转角为
,当旋转角为![]() 时,
时,![]() 与
与![]() 重合,易知
重合,易知![]() ,观察图象可知,在
,观察图象可知,在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长
相应移动的路径长![]() ,由此即可解决问题.
,由此即可解决问题.
解:如图1中,作HM⊥BC于M,设HM=a,则CM=HM=a.
在Rt△ABC中,∠ABC=30°,BC=12,
在Rt△BHM中,BH=2HM=2a,BM=![]() a,
a,
∵BM+FM=BC,
∴![]() a+a=12,
a+a=12,
∴a=6![]() ﹣6,
﹣6,
∴BH=2a=12![]() ﹣12.
﹣12.
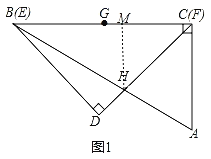
如图2中,当DG⊥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3![]() +3,
+3,
∴HH1=BH﹣BH1=9![]() ﹣15,
﹣15,
当旋转角为60°时,F与H2重合,易知BH2=6![]() ,
,
观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2=18![]() ﹣30+[6
﹣30+[6![]() ﹣(12
﹣(12![]() ﹣12)]=12
﹣12)]=12![]() ﹣18.
﹣18.
故答案为(12![]() ﹣12)cm,(12
﹣12)cm,(12![]() ﹣18)cm.
﹣18)cm.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三位同学到小新家做客,小新用如图所示的一次性茶杯给三位同学分别倒了一杯开水,三个杯子从外观看无任何区别,若三位同学均喝完杯中水后外出玩耍,回来后对水杯放置的位置均已忘记.

(1)现A同学随手从三个已用杯子中拿一个杯子,“拿到自己已用杯子”这一事件是________事件,“拿到大家都没用过的杯子”这一事件是__________事件;
(2)A同学先取一个杯子,B同学在剩下的两个杯子中取一个杯子,求两同学均恰好拿到自己已用杯子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(6,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值( )
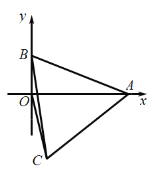
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
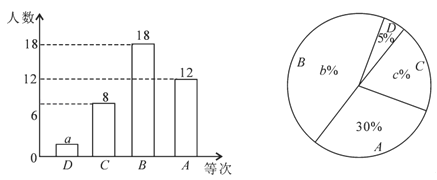
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
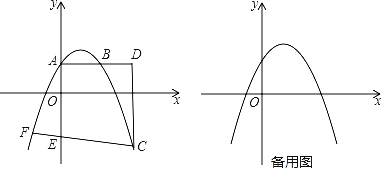
【题目】如图所示,抛物线y=ax2+bx+4的顶点坐标为(3,![]() ),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
(1)求抛物线的函数表达式;
(2)若点E在y轴的负半轴上,且AE=AD,直线CE交抛物线y=ax2+bx+4于点F.
①求点F的坐标;
②过点D作DG⊥CE于点G,连接OD、ED,当∠ODE=∠CDG时,求直线DG的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com