
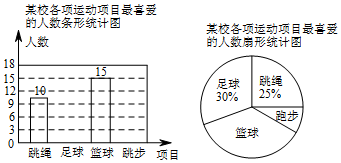
分析 (1)用喜欢跳绳的人数除以其所占的百分比,即可求得被调查的总人数;
(2)用总人数乘以足球所占的百分比即可求得喜欢足球的人数,用总数减去其他各小组的人数即可求得喜欢跑步的人数,从而补全条形统计图;
(3)用360度乘以样本中喜欢足球人数占总人数的比例;
(4)用样本估计总体,即可确定最喜爱篮球的人数.
解答 解:(1)观察条形统计图与扇形统计图可知:喜欢跳绳的有10人,占25%,
故总人数有10÷25%=40人;
(2)喜欢足球的有40×30%=12人,
喜欢跑步的有40-10-15-12=3人,
故条形统计图补充为: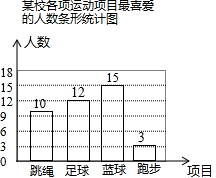
(3)扇形统计图中“足球”所对应扇形的圆心角为360°×$\frac{12}{40}$=108°,
故答案为:108;
(4)全校最喜爱篮球的人数=1200×$\frac{15}{40}$=450,
答:估计全校有450名学生喜爱篮球.
点评 本题考查了扇形统计图、条形统计图及用样本估计总体的知识,解题时注意:用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.解题的关键是能够读懂两种统计图并从中整理出进一步解题的有关信息.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com