
【题目】 如图,平面直角坐标系中,矩形OABC的顶点B的坐标为(7,5),顶点A,C分别在x轴,y轴上,点D的坐标为(0,1),过点D的直线与矩形OABC的边BC交于点G,且点G不与点C重合,以DG为一边作菱形DEFG,点E在矩形OABC的边OA上,设直线DG的函数表达式为y=kx+b
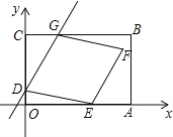
(1)当CG=OD时,求直线DG的函数表达式;
(2)当点E的坐标为(5,0)时,求直线DG的函数表达式;
(3)连接BF,设△FBG的面积为S,CG的长为a,请直接写出S与a的函数表达式及自变量a的取值范围.
【答案】(1)y=4x+1;(2)y=![]() x+1;(3)S=
x+1;(3)S=![]() (7-a)(0<a≤
(7-a)(0<a≤![]() )
)
【解析】
(1)利用矩形的性质结合点B的坐标可得出点A,C的坐标,由点D的坐标结合CG=OD可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(2)利用勾股定理可求出DE的长,由菱形的性质及勾股定理可求出CG的长,进而可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,易证△DCG≌△FME(AAS),利用全等三角形的性质可得出FM的长度,进而可得出FN的长,再利用三角形的面积公式可得出S与a的函数表达式,结合点G不与点C重合及点E在OA上可求出a的取值范围,此题得解.
解:(1)∵四边形OABC为矩形,点B的坐标为(7,5),点A,C分别在x轴,y轴上,
∴点C的坐标为(0,5),点A的坐标为(7,0).
∵点D的坐标为(0,1),CG=OD,
∴点G的坐标为(1,5).
将D(0,1),G(1,5)代入y=kx+b,得:
![]() ,
,
解得:![]() ,
,
∴当CG=OD时,直线DG的函数表达式为y=4x+1.
(2)在Rt△ODE中,OD=1,OE=5,∠DOE=90°,
∴DE=![]() =
=![]() .
.
∵四边形DEFG为菱形,
∴DG=DE=![]() .
.
在Rt△CDG中,DG=![]() ,CD=OC-OD=4,∠DCG=90°,
,CD=OC-OD=4,∠DCG=90°,
∴CG=![]() =
=![]() ,
,
∴点G的坐标为(![]() ,5).
,5).
将D(0,1),G(![]() ,5)代入y=kx+b,得:
,5)代入y=kx+b,得:
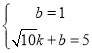 ,
,
解得: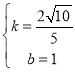 ,
,
∴当CG=OD时,直线DG的函数表达式为y=![]() x+1.
x+1.
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,如图所示.
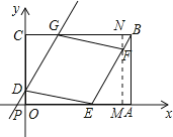
∵DG∥EF,
∴∠FEM=∠GPO.
∵BC∥OA,
∴∠DGC=∠GPO=∠FEM.
在△DCG和△FME中,
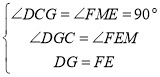 ,
,
∴△DCG≌△FME(AAS),
∴FM=DC=4.
∵MN⊥x轴,
∴四边形OMNC为矩形,
∴MN=OC=5,FN=MN-FM=1.
∵CG的长为a,
∴BG=BC-CG=7-a
∴S=![]() BGFN=
BGFN=![]() (7-a).
(7-a).
∵点E在边OA上,点G在BC边上,且点G不与点C重合,
∴DE≤![]() =5
=5![]() ,a>0,
,a>0,
∴DG=![]() ≤5
≤5![]() ,
,
∴0<a≤![]() .
.
∴S与a的函数表达式为S=![]() (7-a)(0<a≤
(7-a)(0<a≤![]() ).
).


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】南岸区正全力争创全国卫生城区和全国文明城区(简称“两城同创”).某街道积极响应“两城同创”活动,投入一定资金绿化一块闲置空地,购买了甲、乙两种树木共72棵,甲种树木单价是乙种树木单价的![]() ,且乙种树木每棵80元,共用去资金6160元.
,且乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好.该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了a%,乙种树木单价下降了![]() ,且总费用为6804元,求a的值.
,且总费用为6804元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
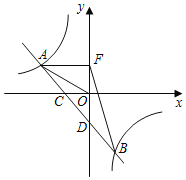
【题目】如图:直线AB与双曲线y=![]() 点交于A、B两点,直线AB与x、y坐标轴分别交于C、D两点,连接OA,若OA=2
点交于A、B两点,直线AB与x、y坐标轴分别交于C、D两点,连接OA,若OA=2![]() ,tan∠AOC=
,tan∠AOC=![]() ,B(3,m)
,B(3,m)
(1)求一次函数与反比例函数解析式;
(2)若点F是点D关于x轴的对称点,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
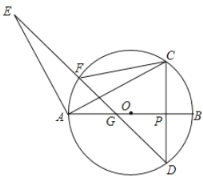
【题目】如图,AB是⊙O的直径,平行四边形ACDE的一边在直径AB上,点E在⊙O上.
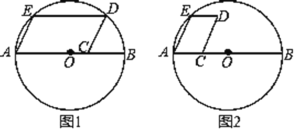
(1)如图1,当点D在⊙O上时,请你仅用无刻度的直尺在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,请你仅用无刻度的直尺在AB上取点Q,使EQ⊥AB于Q.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
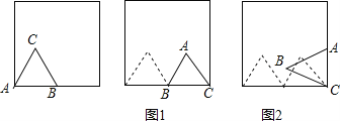
【题目】如图,边长为1的正三角形ABC放置在边长为2的正方形内部,顶点A在正方形的一个顶点上,边AB在正方形的一边上,将△ABC绕点B顺时针旋转,当点C落在正方形的边上时,完成第1次无滑动滚动(如图1);再将△ABC绕点C顺时针旋转,当点A落在正方形的边上时,完成第2次无滑动滚动(如图2),…,每次旋转的角度都不大于120°,依次这样操作下去,当完成第2016次无滑动滚动时,点A经过的路径总长为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
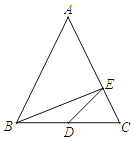
【题目】如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=![]() x2+
x2+![]() B.y=
B.y=![]() x2+
x2+![]()
C.y=![]() x2+2D.y=
x2+2D.y=![]() x2+2
x2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上的一点,过
上的一点,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,并将线段
,并将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,
,![]() ,连接
,连接![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若点![]() 在直径
在直径![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),其它条件不变,请问
重合),其它条件不变,请问![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
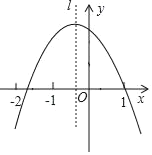
【题目】二次函数y=ax2+bx+c(a≠0),经过点(1.0),对称轴l如图所示,若M=a+b﹣c,N=2a﹣b,P=a+c,则M,N,P中,值小于0的数有( )个.
A.2B.1C.0D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com